Câu 15:

Đây là toán nâng cao chuyên đề bài toán tính tuổi, cấu trúc thi chuyên, thi học sinh giỏi các cấp. Hôm nay, Olm sẽ hướng dẫn các em giải chi tiết dạng này bằng sơ đồ đoạn thẳng như sau:

Giải:

Hiệu số tuổi hai cô cháu bằng: (3 - 1): 1 = \(\frac21\) (tuổi Linh hiện nay)

Coi tuổi Linh hiện nay là 1 phần

ta có sơ đồ:

Theo sơ đồ ta có:

Tuổi Linh hiện nay là: 64:(3 + 2 + 3) = 8 (tuổi)

Tuổi cô Thanh hiện nay là: 8 : \(\frac13\) = 24(tuổi)

Đáp số:

Tuổi Linh hiện nay là: 8 tuổi.

Tuổi cô Thanh hiện nay là 24 tuổi

Ta có sơ đồ câu 15:

Thời gian Như làm mỗi con hạc giấy là:

\(20,4:4=5,1\) (phút) = 5 phút 6 giây

Đáp số: 5 phút 6 giây

3

Giải:

Số có hai chữ số có dạng: \(\overline{ab}\)

Viết thêm chữ số 0 vào giữa hai chữ số của số đó ta được số mới là: \(\overline{a0b}\)

Theo bài ra ta có:

\(\overline{a0b}\) = 6 x \(\overline{ab}\)

100a + b = 60a + b

100a + b - 60a - 6b = 0

(100a - 60a) - (6b - b) = 0

40a - 5b = 0

8a - b = 0

8a = b

b ≤ 9 ⇒ 8a ≤ 9 ⇒ a ≤ 9 : 8 ⇒ a < 2 ⇒ a = 0; 1

Vì a không thể bằng không nên a = 1, b = 8a = 8.1 = 8

Vậy số cần tìm là 18

Giải:

Nếu y tỉ lệ nghịch với x theo tỉ lệ là a thì x cũng tỉ lệ với y theo hệ số tỉ lệ là a

đổi 4 phút 30 giấy=4,5 phút

thời gian Vy làm những tấm thiệp là

4,5 phút x 5 = 22,5 phút

đổi 22,5 phút = 22 phút 30 giây

Đáp số 22 phút 30 giây

Tổng số viên bi trong hộp là:

56x2=112(viên)

Số viên bi đỏ là \(\dfrac{112+20}{2}=\dfrac{132}{2}=66\left(viên\right)\)

Số viên bi xanh là 66-20=46(viên)

Tổng số viên bi trong hộp là:

56×2=112 (viên)

Số viên bi đỏ là:

(112+20) : 2 =66 ( viên )

Số viên bi xanh là:

66-20=42(viên)

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

b: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

=>AH là phân giác của góc BAC

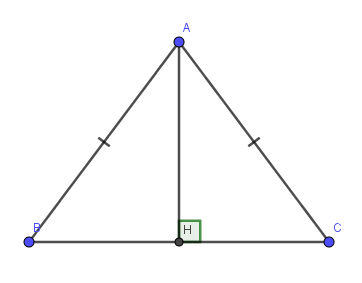
a) Xét hai tam giác vuông: \(\Delta AHB\) và \(\Delta AHC\) có:

\(AB=AC\left(gt\right)\)

\(AH\) là cạnh chung

\(\Rightarrow\Delta AHB=\Delta AHC\) (cạnh huyền - cạnh góc vuông)

b) Do \(\Delta AHB=\Delta AHC\left(cmt\right)\)

\(\Rightarrow\widehat{BAH}=\widehat{CAH}\) (hai góc tương ứng)

\(\Rightarrow AH\) là tia phân giác của \(\widehat{BAC}\)

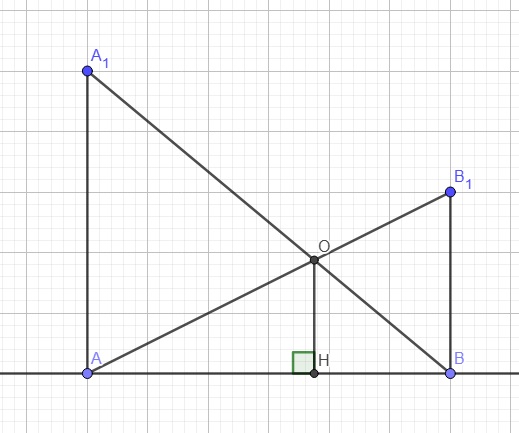
Gọi H là hình chiếu vuông góc của O lên d

\(\Rightarrow AA_1||OH||BB_1\)

Áp dụng định lý Thales trong tam giác \(ABA_1\)

\(\dfrac{OH}{AA_1}=\dfrac{BH}{AB}\)

Áp dụng định lý Thales trong tam giác \(ABB_1\)

\(\dfrac{OH}{BB1}=\dfrac{AH}{AB}\)

\(\Rightarrow\dfrac{OH}{AA_1}+\dfrac{OH}{BB_1}=\dfrac{BH}{AB}+\dfrac{AH}{AB}\)

\(\Rightarrow OH.\left(\dfrac{1}{a}+\dfrac{1}{b}\right)=1\)

\(\Rightarrow OH=\dfrac{a.b}{a+b}\)

Do a, b không đổi \(\Rightarrow OH\) không đổi

Hay khoảng cách từ O đến d không đổi khi A, B chạy trên d