Tam giác đều có cạnh bằng cạnh của hình vuông có diện tích bằng 16cm vuông , bán kính đường tròn ngoại tiếp tam giác đều đó là:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{x+1}=x-2\)
=> \(\left(\sqrt{x+1}\right)^2=\left(x-2\right)^2\)
=> x + 1 = x2 - 4x + 4
<=> x2 - 5x + 3 = 0
<=> \(x^2-2.\frac{5}{2}x+\frac{25}{4}-\frac{13}{4}=0\)
<=> \(\left(x-\frac{5}{2}\right)^2-\left(\frac{\sqrt{13}}{2}\right)^2=0\)
<=> \(\left(x-\frac{5}{2}-\sqrt{\frac{13}{2}}\right)\left(x-\frac{5}{2}+\sqrt{\frac{13}{2}}\right)=0\)
<=> \(\orbr{\begin{cases}x=\frac{5+\sqrt{13}}{2}\\x=\frac{5-\sqrt{13}}{2}\end{cases}}\)
\(ĐK:x-2\ge0\Rightarrow x\ge2\)
Ta có : \(\sqrt{\left(x+1\right)}=x-2\)
\(\left(x+1\right)=\left(x-2\right)^2\)
\(x+1=x^2-4x+4\)
\(x^2-5x+3=0\)
\(\Delta=\left(-5\right)^2-4.3=13\)
Vậy nghiệm của PT là : \(\orbr{\begin{cases}x=\frac{5+\sqrt{13}}{2}\\x=\frac{5-\sqrt{13}}{2}\end{cases}}\)

ĐKXĐ: \(x+1\ne0\)\(\Rightarrow x\ne-1\)
Ta có:\(\left(\frac{x+2}{x+1}\right)^2-\frac{1}{x+1}-3=0\)
<=>\(\frac{x^2+4x+4}{x^2+2x+1}-\frac{x+1}{x^2+2x+1}-\frac{3\left(x^2+2x+1\right)}{x^2+2x+1}=0\)
<=>\(x^2+4x+4-x-1-3\left(x^2+2x+1\right)=0\)
<=>\(x^2+4x+4-x-1-3x^2-6x-3=0\)
<=>\(-2x^2-3x=0\)
<=>\(-x\left(2x+3\right)=0\)
<=>\(\orbr{\begin{cases}-x=0\\2x+3=0\end{cases}}\)
<=>\(\orbr{\begin{cases}x=0\left(TM\right)\\x=\frac{-3}{2}\left(TM\right)\end{cases}}\)
Vậy phương trình có 2 nghiệm x=0 hoặc x=\(\frac{-3}{2}\)

Sợ bạn thật,hỏi cả trên olm vs h luôn
Ta thấy:\(\Delta=\left(m-4\right)^2+12>0\)
Do đó phuognw trình có 2 nghiệm phân biệt với mọi m
Do đó,theo định lý vi-ét,ta có:
\(\Rightarrow\hept{\begin{cases}x_1x_2=-3\\x_1+x_2=m-4\end{cases}}\)
Vì \(x_1x_2=-3< 0\)nên x1 và x2 trái dấu nhau
Giả sử x1<0 do đó x2>0
\(\Rightarrow\left|x_2\right|=x_2\)
\(\Rightarrow x_1-\left|x_2\right|< 0\Rightarrow10< 0\left(L\right)\)
Như vậy suy ra\(\hept{\begin{cases}x_1>0\\x_2< 0\Rightarrow\left|x_2\right|=-x_2\end{cases}}\)
\(\Rightarrow x_1-\left|x_2\right|=x_1+x_2=10\)
Mà \(x_1+x_2=m-4\)
\(\Rightarrow m-4=10\Rightarrow m=14\)
Vậy khi m=14 thì pt có 2 nghiệm phân biệt

Đặt \(\frac{\sqrt{x}}{x-4}=a\left(a\inℤ\right)\)
Nếu x không là số chính phương,ta có:
\(\Rightarrow\sqrt{x}=\left(x-4\right)a\)
Mặt khác;\(\hept{\begin{cases}\sqrt{x}\notinℤ\\\left(x-4\right)a\inℤ\end{cases}}\)
Suy ra mâu thuẫn
Do đó,x là số chính phương.
\(\Rightarrow\sqrt{x}\inℤ\)
Ta lại có :Để \(\frac{\sqrt{x}}{x-4}\inℤ\Leftrightarrow\sqrt{x}⋮x-4\Rightarrow\left(\sqrt{x}\right)^2⋮x-4\)
\(\Leftrightarrow\left(x-4\right)+4⋮x-4\)
\(\Rightarrow4⋮x-4\)
Mà x là số nguyên nên x-4 là số nguyên
\(\Rightarrow x-4\in\left\{\pm1;\pm2;\pm4\right\}\)
\(\Rightarrow x\in\left\{0;2;3;5;6;8\right\}\)
Mà x là số chính phương nên x=0(thỏa mãn)
Vậy khi x=0 thì \(\frac{\sqrt{x}}{x-4}\inℤ\)

Điều kiện : \(x\ge0\)
\(B=\frac{2x}{x+3\sqrt{x}+2}+\frac{5\sqrt{x}+1}{x+4\sqrt{x}+3}+\frac{\sqrt{x}+10}{x+5\sqrt{x}+6}\)
\(=\frac{2x\left(\sqrt{x}+3\right)+\left(5\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+\left(\sqrt{x}+10\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\sqrt{x}+6x+5x+11\sqrt{x}+2+x+11\sqrt{x}+10}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\sqrt{x}+12x+22\sqrt{x}+12}{\left(x+3\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2\left(x\sqrt{x}+6x+11\sqrt{x}+6\right)}{x\sqrt{x}+6x+11\sqrt{x}+6}=2\)
Vậy \(B=2\)
\(B=\frac{2x}{x+3\sqrt{x}+2}+\frac{5\sqrt{x}+1}{x+4\sqrt{x}+3}+\frac{\sqrt{x}+10}{x+5\sqrt{x}+6}\)
\(=\frac{2x}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)}+\frac{5\sqrt{x}+1}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+3\right)}+\frac{\sqrt{x}+10}{\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\left(\sqrt{x}+3\right)+\left(5\sqrt{x}+1\right)\left(\sqrt{x}+2\right)+\left(\sqrt{x}+10\right) \left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\sqrt{x}+6x-5x+11\sqrt{x}+2+x+11\sqrt{x}+10}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)
\(=\frac{2x\sqrt{x}+2x+22\sqrt{x}+12}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}=\frac{2\left(x\sqrt{x}+x+11\sqrt{x}+6\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}+2\right)\left(\sqrt{x}+3\right)}\)

\(A=\left(\frac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\frac{\sqrt{x}-2}{x-1}\right).\frac{x\sqrt{x}+x-\sqrt{x}-1}{\sqrt{x}}\)ĐK : \(x\ne0;1\)
\(=\left(\frac{\sqrt{x}+2}{\left(\sqrt{x}+1\right)^2}-\frac{\sqrt{x}-2}{\left(\sqrt{x}\pm1\right)}\right).\frac{\sqrt{x}\left(x-1\right)+x-1}{\sqrt{x}}\)
\(=\left(\frac{\left(\sqrt{x}+2\right)\left(\sqrt{x}-1\right)-\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)^2\left(\sqrt{x}-1\right)}\right).\frac{\left(\sqrt{x}+1\right)\left(x-1\right)}{\sqrt{x}}\)
\(=\frac{x+\sqrt{x}-2-\left(x-\sqrt{x}-2\right)}{\sqrt{x}}=\frac{2\sqrt{x}}{\sqrt{x}}=2\)
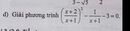
-từ S hình vuông => cạnh tam giác =4
- BK= \(R=\frac{1}{2}.\frac{4}{\cos30}=\frac{4}{\sqrt{3}}\left(cm\right)\)