Để tìm giao của hai tập hợp A và B, ta cần xác định phần nằm trong cả hai tập hợp. Ta có:

A = (-2;7]

B = [0;5]

Phần nằm trong cả hai tập hợp là đoạn [-2;5], vì nó nằm trong A và cũng nằm trong B.

Vậy, ta có:

A ∩ B = [-2;5]

CAB là bù của A ∩ B trong tập hợp A hoặc B. Vì vậy, ta có:

CAB = (-∞;-2) U (5;7]

Vậy đáp án là D.CAB=(-2;0)U(5;7].

Để tìm giao của hai tập hợp A và B, ta cần xác định phần nằm trong cả hai tập hợp. Ta có:

A = (-2;7]

B = [0;5]

Phần nằm trong cả hai tập hợp là đoạn [-2;5], vì nó nằm trong A và cũng nằm trong B.

Vậy, ta có:

A ∩ B = [-2;5]

CAB là bù của A ∩ B trong tập hợp A hoặc B. Vì vậy, ta có:

CAB = (-∞;-2) U (5;7]

Vậy đáp án là D.CAB=(-2;0)U(5;7].

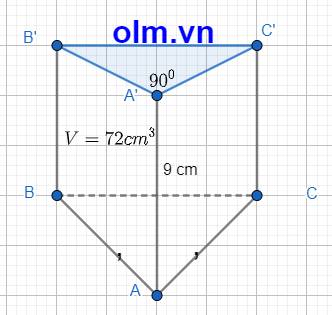
V_ABCA'B'C'  = S_ABC.h

Diện tích của tam giác ABC là: 72 : 9 = 8 (cm²)

S_ABC = \(\dfrac{1}{2}\)AB.AC = \(\dfrac{1}{2}\)AB² = 8 ⇒ AB² = 8.2 = 16 

⇒ AB = AC = \(\sqrt{16}\) = 4 (cm)

Vậy độ dài cạnh đáy AB dài 4cm

Gọi số ti vi mỗi loại mà cửa hàng bán được lần lượt là:

\(x;y;z\) (chiếc) \(x;y;z\) \(\in\)N^*

Thì số tiền thu được được việc bán mỗi loại ti vi lần lượt là:

20\(x;\) 18\(y\); 15\(z\) 

Theo bài ra ta có: 20\(x\) = 18\(y\) = 15\(z\);    \(x+y+z=62\)

⇒ \(y\) = \(\dfrac{20}{18}\)\(x\) = \(\dfrac{10}{9}\)\(x\)

    z = \(\dfrac{20}{15}\)\(x\) = \(\dfrac{4}{3}x\)

⇒ \(x+\dfrac{10}{9}x+\dfrac{4}{3}x=62\)

    \(x\left(1+\dfrac{10}{9}+\dfrac{4}{3}\right)=62\)

    \(\dfrac{31}{9}\)\(x\)                      = 62

        \(x\)                      = 62: \(\dfrac{31}{9}\)

        \(x\)                      =  18

         \(y\) = \(\dfrac{10}{9}.18=20\)

        \(z=\dfrac{4}{3}.18=24\)

Kết luận: Ti vi sam sung bán được 18 chiếc

                Ti vi LG bán được 20 chiếc

                Ti vi Xiaomi bán được 24 chiếc

\(x+567+x-67=x+90\\ \Rightarrow\left(x+x\right)+\left(567-67\right)=x+90\\ \Rightarrow2x+500-x-90=0\\ \Rightarrow x+410=0\\ \Rightarrow x=-410\)

`x+567 +x-67=x+90`

`=>(x+x)+(567-67)=x+90`

`=>2x+500=x+90`

`=>2x-x=90-500`

`=>x= - 410`

Vậy `x=-410`

vì các số lẻ liên tiếp cách nhau 2 đơn vị => có số số lẻ liên tiếp từ 211 đến 971 là (971-211): 2 +1=381 số          Cho mình 5 sao nha

  Đáp Án :Vì các số lẻ liên tiếp cách nhau 2 đơn vị => có số số lẻ liên tiếp từ 211 đến 971 là (971-211): 2 +1=381 số  

\(\dfrac{2n-3}{n+1}=\dfrac{2\left(n+1\right)-5}{n+1}=2-\dfrac{5}{n+1}\)

Để \(\left(2n-3\right)⋮\left(n+1\right)\Rightarrow5⋮\left(n+1\right)\)

=> \(\left(n+1\right)=\left\{-5;-1;1;5\right\}\Rightarrow n=\left\{-6;-2;0;4\right\}\)

n=(-6;-2;0;4)

 Ta thấy rằng \(\dfrac{BN}{BC}=\dfrac{AQ}{AD}\), mà \(BC=AD\) nên \(BN=AQ\), cũng có nghĩa ABNQ và CDQN là các hình chữ nhật. Ta kẻ MH và PK vuông góc với QN. Khi đó \(S_{MNPQ}=S_{MNQ}+S_{PNQ}\) 

\(=\dfrac{1}{2}\times PQ\times MH+\dfrac{1}{2}\times PQ\times PK\) 

\(=\dfrac{1}{2}\times PQ\times\left(MH+PK\right)\) 

\(=\dfrac{1}{2}\times AB\times BC\) (do \(PQ=AB\) và \(MH+PK=BC\))

\(=\dfrac{1}{2}\times S_{ABCD}\)

\(=\dfrac{1}{2}\times324=162\left(cm^2\right)\)

Phải sửa lại như thế này nhé. Nãy mình nhầm.

vì (x-7)(x+3)<0

=> (x-7) và (x+3) phải trái dấu

=> nếu x-7 < 0 thì x+3 >0

nếu x-7 >0 thì x+3<0

+ xét trường hợp 1 

=>x-7<0 =>x<7

  x+3>0 => x >-3

hay -3<x<7 ( thõa mãn)

+ xét trường hợp 2:

=> x-7>0 => x>7

     x+3<0 = >x<-3

=> vô lí x ko thể lớn hơn 7 mà bé hơn -3

vậy -3<x<7 (bạn tự liệt kê)

Vì (x-7)(x+3)<0

(x-7) phải có dấu (x+3)

Nếu x-7<0 thì x+3>0 

- Xét trường hợp x-7<0 thì x+3>0

x-7<0 vậy x<7

x+3>0 vẫy>-3

-3<x<7

Tổng 3 số là

(2x19+2x16+2x15):2=50

Tổng số thứ 1 và thứ 2 là

19x2=38

Số thứ 3 là

50-38=12

Số thứ nhất là

2x15-12=18

Số thứ 2 là

50-(18+12)=20

333333

\(xy-5y+5x-24=12\\ =>y\left(x-5\right)+5\left(x-5\right)+1=12\\ =>\left(x-5\right)\left(y+5\right)=11\)

Bổ sung đề : x,y nguyên 

=> x-5,y+5 thuộc Z

Ta có : 11=1.11=(-1).(-11)

Đến đây bạn lập bảng giá trị ra rồi tìm x,y.

xy-5y+5x-24=12

y(x-5)+5(x-5)+1=12

(x-5)(y+5)=11

x,y nguyên

x-5, y+5 thuộc Z

mình chỉ biết làm tới đây thui