Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



A = 2 - 3 - 4 + 5 + 6 - 7 - 8 + 9 + ... + 2018 - 2019 - 2020
Xét dãy số: 2; 3; 4;...; 2019; 2020
Dãy số trên có số số hạng là:
(2020 - 2) : 1 + 1 = 2019
Vì 2019 : 4 = 504 dư 3
Nhóm 4 số hạng liên tiếp của A vào nhau khi đó:
A = (2-3-4+5)+(6-7-8+9)+ ...+(2014 - 2015 - 2016+2017) + (2018 - 2019 - 2020)
A = 0 + 0 + ...+ 0 + (-1 - 2020)
A = - 2021

A = \(\frac13\) + \(\frac16\) + \(\frac{1}{10}\) + \(\frac{1}{15}\) + ... + \(\frac{1}{45}\)
A = \(\frac26\) + \(\frac{2}{12}\) + \(\frac{2}{20}\) + \(\frac{2}{30}\) + ... + \(\frac{2}{90}\)
A = 2.(\(\frac{1}{2.3}\) + \(\frac{1}{3.4}\) + \(\frac{1}{4.5}\) + ... + \(\frac{1}{9.10}\))
A = 2.(\(\frac12-\frac13\) + \(\frac13-\frac14\) +\(\frac14-\) \(\frac15\) + ... + \(\frac19\) - \(\frac{1}{10}\))
A = 2.(\(\frac12-\frac{1}{10}\))
A = 2.\(\frac25\)
A = \(\frac45\)

a: Trong cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOt}< \widehat{xOy}\left(50^0< 120^0\right)\)
nên tia Ot nằm giữa hai tia Ox và Oy
=>\(\widehat{xOt}+\widehat{yOt}=\widehat{xOy}\)
=>\(\widehat{yOt}=120^0-50^0=70^0\)
b: Ta có: \(\widehat{xOy}+\widehat{x'Oy}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Oy}=180^0-120^0=60^0\)
Ta có: \(\widehat{xOt}+\widehat{x'Ot}=180^0\)(hai góc kề bù)
=>\(\widehat{x'Ot}=180^0-50^0=130^0\)

\(x>9,99\) nên \(x\in\left\{10,11,12,...\right\}\)
Mà x bé nhất nên \(x=10\)

\(\dfrac{3}{5}+\dfrac{4}{7}\times\dfrac{14}{6}\)
\(=\dfrac{3}{5}+\dfrac{56}{42}\)
\(=\dfrac{3}{5}+\dfrac{4}{3}=\dfrac{9}{15}+\dfrac{20}{15}=\dfrac{29}{15}\)

\(\dfrac{3}{5}-\dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=\dfrac{4}{5}\\ \dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=\dfrac{3}{5}-\dfrac{4}{5}\\ \dfrac{1}{5}\cdot\left(x-\dfrac{1}{2}\right)=-\dfrac{1}{5}\\ x-\dfrac{1}{2}=-\dfrac{1}{5}:\dfrac{1}{5}\\ x-\dfrac{1}{2}=-1\\ x=-1+\dfrac{1}{2}\\ x=-\dfrac{1}{2}\)
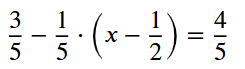
\(\dfrac{x-1}{2023}-\dfrac{1}{10}-\dfrac{1}{15}-\dfrac{1}{21}-...-\dfrac{1}{120}=\dfrac{5}{8}\)
=>\(\dfrac{x-1}{2023}-\left(\dfrac{1}{10}+\dfrac{1}{15}+...+\dfrac{1}{120}\right)=\dfrac{5}{8}\)
=>\(\dfrac{x-1}{2023}-2\left(\dfrac{1}{20}+\dfrac{1}{30}+...+\dfrac{1}{240}\right)=\dfrac{5}{8}\)
=>\(\dfrac{x-1}{2023}-2\left(\dfrac{1}{4}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{6}+...+\dfrac{1}{15}-\dfrac{1}{16}\right)=\dfrac{5}{8}\)
=>\(\dfrac{x-1}{2023}-2\left(\dfrac{1}{4}-\dfrac{1}{16}\right)=\dfrac{5}{8}\)
=>\(\dfrac{x-1}{2023}-2\cdot\dfrac{3}{16}=\dfrac{5}{8}\)
=>\(\dfrac{x-1}{2023}=\dfrac{5}{8}+\dfrac{3}{8}=\dfrac{8}{8}=1\)
=>x-1=2023
=>x=2024