Lời giải:

Áp dụng BĐT AM-GM:

$x^2+2^2\geq 4x$

$y^2+2^2\geq 4y$

$2(x^2+y^2)\geq 4xy$

$\Rightarrow 3(x^2+y^2)+8\geq 4(x+y+xy)=32$

$\Rightarrow x^2+y^2\geq 8$

Vậy $P_{\min}=8$ khi $x=y=2$

Lời giải:
$(\sqrt{2}x+\sqrt{8}y)^2=(\sqrt{2}x)^2+(\sqrt{8}y)^2+2\sqrt{2}x.\sqrt{8}y$

$=2x^2+8y^2+8xy$

Đề yêu cầu gì đó em?

A B C D

\(\widehat{A}+\widehat{D}=70^o+110^o=180^o\) 

=> ABCD là tứ giác nội tiếp (tứ giác có tổng 2 góc đối =180 là tứ giác nt)

\(\widehat{ABD}=\widehat{ACD}\) (góc nt cùng chắn cung AD) (1)

\(\widehat{CBD}=\widehat{CAD}\) (góc nt cùng chắn cung CD) (2)

Tg ADC cân tại D \(\Rightarrow\widehat{ACD}=\widehat{CAD}\) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{ABD}=\widehat{CBD}\)

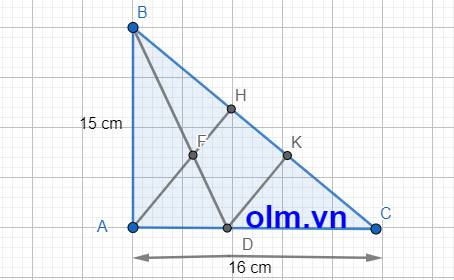
a, Xét \(\Delta\)BAH và \(\Delta\)BCA có: \(\widehat{ABC}\)  chung; \(\widehat{AHB}\) = \(\widehat{BAC}\) = 90⁰

⇒\(\Delta\)BAH \(\sim\)\(\Delta\)BCA (g-g)

⇒\(\dfrac{BA}{BC}=\dfrac{AH}{CA}=\dfrac{BH}{BA}\)

b, Theo pytago ta có: BC² = AB² + AC² = 15²+16² = 481 (cm²)

⇒ BC = \(\sqrt{481}\) cm

Kẻ đường cao DK vuông góc với BC cắt BC tại K 

DA = DK ( vì mọi điểm trên tia phân giác thì cách đều hai cạnh còn lại)

Vì \(\Delta\)ABD và \(\Delta\)BCD có đường cao bằng nhau nên tỉ số diện tich hai tam giác bằng tỉ số hai cạnh đáy và bằng:

\(\dfrac{AB}{BC}\) = \(\dfrac{15}{\sqrt{481}}\)  

Tương tự ta có tỉ số diện tích hai tam giác, tam giác ABD và tam giác BCD bằng:

\(\dfrac{AD}{DC}\) ⇒ \(\dfrac{AD}{DC}\) = \(\dfrac{15}{\sqrt{481}}\) ⇒ \(\dfrac{AD}{15}\) = \(\dfrac{DC}{\sqrt{481}}\) 

Áp dụng tính chất dãy tỉ số bằng nhau ta có:

\(\dfrac{AD}{15}\) = \(\dfrac{DC}{\sqrt{481}}\) = \(\dfrac{AD+DC}{15+\sqrt{481}}\) = \(\dfrac{16}{15+\sqrt{481}}\) 

AD = \(\dfrac{16}{15+\sqrt{481}}\)\(\times\)15 = \(\dfrac{240}{15+\sqrt{481}}\) = \(\dfrac{15}{16}\)(\(\sqrt{481}\) - 15)

DC = \(\dfrac{16}{15+\sqrt{481}}\) \(\times\) \(\sqrt{481}\) = \(\dfrac{1}{16}\)(481 - 15\(\sqrt{481}\))

Đổi 120 000 l = 120 m³ 

Chiều cao của hồ nước cũng chính là độ sâu của hồ và bằng:

120 : ( 8 \(\times\) 3) = 5 (m)

Kết luận chiều sâu của hồ nước là 5m 

Đổi \(120000l=120m^3\)

Ta có : \(V=d.r.h\Rightarrow h=\dfrac{V}{d.r}=\dfrac{120}{8.3}=\dfrac{120}{24}=5\left(m\right)\)

Vậy độ sâu của hồ nước là 5m.

Cái bạn viết chưa phải 1 phương trình nhé. Bạn xem lại.

ò ra vậy thank bạn