Lời giải:
Vì $x+1, y+2013$ chia hết cho $6$ nên đặt $x+1=6k, y+2013=6m$ với $k,m\in\mathbb{N}^*$ 

Khi đó:

$4^{x}+x+y=4^{6k-1}+6k-1+6m-2013$

$=4^{6k-1}-2014+6(k+m)$

Vì $4\equiv 1\pmod 3$

$\Rightarrow 4^{6k-1}\equiv 1^{6k-1}\equiv 1\pmod 3$

$\Rightarrow 4^{6k-1}-2014\equiv 1-2014\equiv -2013\equiv 0\pmod 3$

$\Rightarrow 4^{6k-1}-2014\vdots 3$

Mà $4^{6k-1}-2014$ chẵn với mọi $k\in\mathbb{N}^*$

$\Rightarrow 4^{6k-1}-2014\vdots 6$

Kết hợp với $6k+6m\vdots 6$

$\Rightarrow 4^x+x+y=4^{6k-1}-2014+6k+6m\vdots 6$ (đpcm) 

Bài 3:

a, (\(x\)+y+z)²

=((\(x\)+y) +z)²

= (\(x\) + y)² + 2(\(x\) + y)z + z²

= \(x^2\) + 2\(xy\) + y² + 2\(xz\) + 2yz + z²

=\(x^2\) + y² + z² + 2\(xy\) + 2\(xz\) + 2yz

b, (\(x-y\))(\(x^2\) + y² + z² - \(xy\) - yz - \(xz\))

= \(x^3\) + \(xy^2\) + \(xz^2\) - \(x^2\)y - \(xyz\) - \(x^2\)z - y³ 

Đến dây ta thấy xuất hiện \(x^3\) - y³ khác với đề bài, em xem lại đề bài nhé

|\(x\)| = 1 ⇒ (|\(x\)|)² = 1 ⇒ \(x^2\) = 1

Thay \(x^2\) = 1 vào biểu thức: M = (\(x^{2^{ }}\) + a)(\(x^2\) + b)(\(x^2\) + c) ta có:

M = (1 + a)(1 + b)(1 + c)

M = (1 + b + a + ab)(1 + c)

M = 1 + b + a + ab + c + bc + ac + abc

M = 1 + ( a + b + c) + (ab + bc + ac) + abc

M = 1 + 2 + (-5) +  3

M = (1+2+3) - 5

M = 1

|\(x\)| = 1 ⇒ \(x^2\) = 1

Thay \(x\)² =  1 vào biểu thức M ta có:

M = (1 + a)(1 +b)(1+c)

M = ( 1 + b + a + ab)(1 + c)

M = 1 + b + a + ab + c + bc + ac + abc

M = 1 + (a+b+c) + (ab+bc + ac) + abc

M = 1 + 2 - 5 + 3

M = 1

a, 

   (\(x\) + y + z)²

 = ((\(x\) + y) + z)² 

= (\(x\)+y)²+2(\(x\)+y)z+ z² 

= \(x^2\) + 2\(x\)y+ y² + 2\(x\)z + 2yz + z²

= \(x^2\) + y² + z² + 2\(xy\) + 2yz + 2\(x\)z

b, (\(x\)+y+z)(\(x^2\) + y² + z² - \(xy\) - yz - \(x\)z) 

= \(x^3\) + \(x\)y² + \(x\)z² - \(x^2\)y - \(x\)yz - \(x^2\)z + y\(x^2\) + y³ + yz² - \(x\)y² - y²z - \(xyz\) +

+ z\(x^2\) + zy² + z³ - \(xyz\) - yz² - \(x\)z²

= \(x^{3^{ }}\)+y³+z³ - 3\(x\)yz + (\(x\)z² - \(x\)z²) - (\(x^2\)y- \(x^2\)y) - (\(x^2\)z - \(x^{2^{ }}\)z) + (y²\(x\) - y²\(x\)) - (y²z - y²z) + (z²y - z²y)

= \(x^3\) + y³ + z³ - 3\(xyz\)

c, 

 VT =  (\(x\) + y + z)³ 

VT = (\(x\) + y)³ + 3(\(x\)+y)²z + 3(\(x\) +y)z² + z³

VT = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y³ + 3(\(x\)+y)z(\(x+y+z\)) + z³

VT = \(x^3\)+ y³ + z³ + 3\(xy\)(\(x\) +y)  + 3(\(x+y\))z(\(x+y+z\))

VT = \(x^3\) + y³ + z³ + 3(\(x+y\))(\(xy\) + z\(x\) + zy + z²)

VT = \(x^3\) + y³ + z³ + 3(\(x\) + y){ (\(xy+xz\)) + (zy +z²)

VT = \(x^3\) + y³ + z³ + 3(\(x\) + y){ \(x\) (y+z) + z(y+z)}

VT = \(x^3\) + y³ + z³ + 3(\(x\) + y)(y+z)(\(x+z\))

VT = VP (đpcm)

Bài 1: 

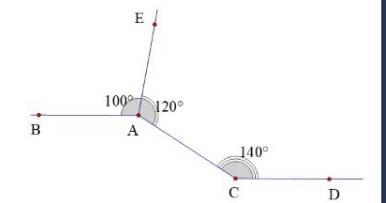
Ta có \(\widehat{BAC}\) = 360⁰ - 100⁰ - 120⁰ = 140⁰

       ⇒\(\widehat{BAC}\) = \(\widehat{ACD}\) = 140⁰

⇒ AB//CD 

Bài 16:

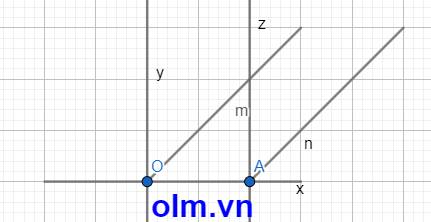
Oy \(\perp\) Ox 

Az \(\perp\) Ox 

⇒ Oy // Az (vì hai đường thẳng phân biệt cùng vuông góc với đường thẳng thứ ba thì chúng song song song với nhau).

Ta có \(\widehat{AOm}\) = 90⁰ : 2 = 45⁰ ( vì Om là phân giác của \(\widehat{xOy}\))

         \(\widehat{xAn}\) = 90⁰ : 2 = 45⁰ (vì An là phân giác của \(\widehat{xAz}\))

   \(\Rightarrow\) \(\widehat{AOM}\) = \(\widehat{xAn}\) 

    \(\Rightarrow\) Om //On ( vì hai đường thẳng cùng cắt đường thẳng thứ ba tạo thành hai góc đồng vị bằng nhau) 

Số số chẵn là: 16 + 2 = 18 (số chẵn)

Hiệu hai số là: 2 \(\times\)( 18 - 1) = 34

Ta có sơ đồ: 

Theo sơ đồ ta có:

Số chẵn bé là: (206 - 34): 2 = 86

Số chẵn lớn là: 86 + 34 = 130

Đáp sô: số chẵn bé 86

             số chẵn lớn 130

Đăng có nhiều hơn Tuấn 67 viên bi. Sau khi Đăng cho Tuấn một số viên bi thì Đăng có it hơn Tuấn 8 viên bi. Hỏi Đăng cho Tuấn bao nhiêu viên bi ?

Các bạn hãy giúp mình đi ! 

Số số chẵn là: 2 + 2 = 4 (số chẵn)

Hiệu hai số chẵn cần tìm là: 2\(\times\)(4-1) = 6

Ta có sơ đồ:

Theo sơ đồ ta có:

Số chẵn lớn là: ( 30 + 6): 2 = 18

Số chẵn bé là: 18 -  6 = 12

Đáp số: số chẵn bé 12

             số chẵn lớn 18

♩  ♬  |  ♬  ♩  |  ♩  ∞  |  ♩  ∞ ||

Tuổi mẹ và tuổi con hiện nay là:

44 + 4 \(\times\) 2 = 52 (tuổi)

Ta có sơ đồ:

Theo sơ đồ ta có, tuổi con hiện nay là: 

(52 - 30):2 = 11 (tuổi)

Tuổi mẹ hiện nay là: 

11 + 30 = 43 (tuổi)

Đáp số: Tuổi mẹ hiện nay 41 tuổi

             Tuổi con hiện nay 11 tuổi

Bài 1 :

\(A=-x^2+6x+14\)

\(A=-x^2+6x-9+23\)

\(A=-\left(x^2-6x+9\right)+23\)

\(A=-\left(x-3\right)^2+23\)

Vì \(-\left(x-3\right)^2\le0\)

\(\Rightarrow A=-\left(x-3\right)^2+23\le23\)

\(\Rightarrow Max\left(A\right)=23\)

Bài 2 :

\(B=4x^2+12x+30\)

\(\Rightarrow B=4x^2+12x+9+21\)

\(\Rightarrow B=\left(2x+3\right)^2+21\)

Vì \(\left(2x+3\right)^2\ge0\)

\(\Rightarrow B=\left(2x+3\right)^2+21\ge21\)

\(\Rightarrow Min\left(B\right)=21\)