Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Sau ngày thứ nhất cửa hàng còn:
\(1-\dfrac{1}{3}=\dfrac{2}{3}\) (số gạo)
Sau ngày thứ hai cửa hàng còn:
\(\dfrac{2}{3}-\dfrac{3}{5}=\dfrac{1}{15}\) (số gạo)
Ban đầu cửa hàng có số gạo là:
\(16:\dfrac{1}{15}=240\left(kg\right)\)
ĐS: ...

a) Trong mặt phẳng (SAC), gọi I là giao điểm của AO và MN. Khi đó vì \(MN\subset\left(BMN\right)\) nên I chính là giao điểm của (BMN) và SO.
b) Ta có \(I\in SO\subset\left(SBD\right)\) nên \(I\in\left(SBD\right)\). Trong mặt phẳng (SBD), gọi K là giao điểm của BI và SD. Khi đó vì \(K\in BI\subset\left(BMN\right)\) nên K chính là giao điểm của (BMN) và SD.
a: Trong mp(SAC), gọi K là giao điểm của MN với SO
mà MN\(\in\left(BMN\right)\)
nên \(K=SO\cap\left(BMN\right)\)
b: Vì K là giao của MN và SO
mà \(MN\in\left(BMN\right);SO\in\left(SBD\right)\)
nên \(K\in\left(BMN\right)\cap\left(SBD\right)\)
mà \(B\in\left(BMN\right)\cap\left(SBD\right)\)
nên \(\left(BMN\right)\cap\left(SBD\right)=BK\)
Gọi E là giao điểm của BK với SD
=>K là giao điểm của SD với (BMN)

1) 15.9^3 : 27 - 6^2.12 +18.41
= 15.729 : 27 - 36.12 +738
= 10935 : 27 - 432 + 738
= 405 - 432 + 738
= 711
2) 18.7^3 + 9.2^6 :8 - 12.7
= 18.343 + 9.64 :8 - 84
= 6174 + 72 - 84
= 6162
3) 23.2^5 + 288.4^2 :12
= 23.32 + 288.16 :12
= 736 + 384
= 1120
4) 12^2 : 36 + 8^2 : 4 - 5.3
= 144 : 36 + 64 : 4 - 15
= 4 + 16 - 15
= 5

\(x+10\%\cdot x+20\%\cdot x+30\%\cdot x=4,8\)
=>\(x\left(1+0,1+0,2+0,3\right)=4,8\)
=>\(x\cdot1,6=4,8\)
=>\(x=4.8:1.6=3\)

\(\overline{ab5}=\overline{ab}+230\)
=>\(10\overline{ab}+5=\overline{ab}+230\)
=>\(9\overline{ab}=225\)
=>\(\overline{ab}=25\)
Vậy: a=2;b=5

Số số hạng là \(\dfrac{20-2}{2}+1=10\left(số\right)\)
Tổng của dãy số 2;4;6;...;20 là:
\(\left(20+2\right)\times\dfrac{10}{2}=110\)
(y+2)+(y+4)+...+(y+20)=160
=>10y+110=160
=>10y=50
=>y=50:10=5
(y+2)+(y+4)+...+(y+20)=160
y+2+y+4+...+y+20=160
(y+y+...+y)+(2+4+...+20)=160
10 x y + 110 = 160
10 x y = 160 - 110
10 x y = 50
y = 50 : 10 = 5

\(\left(-2x^2y\right)^2\cdot8x^3\cdot yz^3\\ =\left(-2\right)^2\cdot\left(x^2\right)^2\cdot y^2\cdot8x^3\cdot yz^3\\ =4x^4y^2\cdot8x^3\cdot yz^3\\ =4\cdot8\cdot\left(x^4\cdot x^3\right)\cdot\left(y^2\cdot y\right)\cdot z^3\\ =32x^7y^3z^3\)
`#3107.101107`
\((-2x^2y)^2\cdot8x^3\cdot yz^3 \\ = 4x^4y^2 \cdot8x^3 \cdot yz^3 \\ = (4 \cdot 8) \cdot (x^4y^2 \cdot x^3 \cdot yz^3) \\ = 32x^7y^3z^3\)
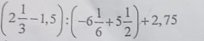
a: \(0,5^{1000}=\left(0,5^5\right)^{200}=0,03125^{200}\)
mà \(0,03125< 0,625\)
nên \(0,5^{1000}< 0,625^{200}\)
c: \(A=2+2^2+...+2^{2022}\)
=>\(2A=2^2+2^3+...+2^{2023}\)
=>\(2A-A=2^2+2^3+...+2^{2023}-2-2^2-...-2^{2022}\)
=>\(A=2^{2023}-2\)
=>A<B
e: \(2020A=\dfrac{2020^{2024}-2020}{2020^{2024}-1}=1-\dfrac{2019}{2020^{2024}-1}\)
\(2020B=\dfrac{2020^{2024}+2020}{2020^{2024}+1}=1+\dfrac{2019}{2020^{2024}+1}\)
Vì \(-\dfrac{2019}{2020^{2024}-1}< 0< \dfrac{2019}{2020^{2024}+1}\)
nên \(-\dfrac{2019}{2020^{2024}-1}+1< \dfrac{2019}{2020^{2024}+1}+1\)
=>2020A<2020B
=>A<B
d: \(\left(-\dfrac{3}{2}\right)^{2024}=\left(\dfrac{3}{2}\right)^{2024};\left(-2\right)^{2024}=2^{2024}\)
mà 3/2<2
nên \(\left(-\dfrac{3}{2}\right)^{2024}< 2^{2024}\)