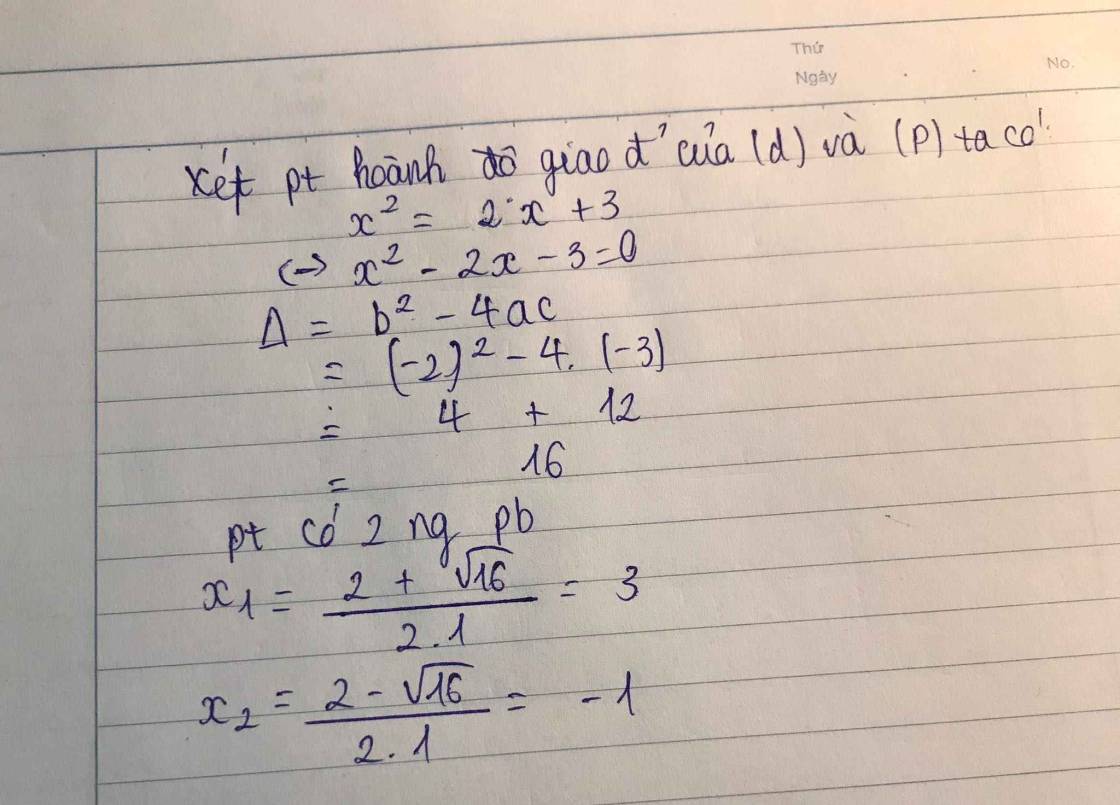Vì có ghỉ 20 phút nên thời gian đến nếu ko nghỉ là 4 giờ 25 phút Mà xuất phát từ 22 giờ nên ô tô đi trong 6 giờ 25 phút Đổi 6 giờ 25 phút = 6\(\dfrac{5}{12}\) giờ Quãng đường AB là 45 x 6\(\dfrac{5}{12}\) =288,75 km

pt đã cho \(\Leftrightarrow\sqrt{\left(x-1\right)^2+1}+\sqrt{3\left(x-1\right)^2+4}=3-\sqrt{x-1}\) Vì \(\left(x-1\right)^2\ge0\Leftrightarrow\left(x-1\right)^2+1\ge1\Leftrightarrow\sqrt{\left(x-1\right)^2+1}\ge1\) Tương tự, ta có \(\sqrt{3\left(x-1\right)^2+4}\ge2\)  Từ đó, ta có \(VT\ge3\) \(\Leftrightarrow VP\ge3\) \(\Leftrightarrow3-\sqrt{x-1}\ge3\) \(\Leftrightarrow\sqrt{x-1}\le0\) Lại có \(\sqrt{x-1}\ge0\) \(\Rightarrow\sqrt{x-1}=0\)\(\Leftrightarrow x-1=0\Leftrightarrow x=1\) Vậy tập nghiệm của pt đã cho là \(S=\left\{1\right\}\)

a) Dễ thấy \(\widehat{AMC}=90^o\) Xét (O) có đường kính AB \(\Rightarrow\) \(\widehat{ANB}\) là góc nội tiếp chắn nửa đường tròn. \(\Rightarrow\widehat{ANB}=90^o\) hay \(\widehat{ANC}=90^o\) Tứ giác ANCM có \(\widehat{AMC}+\widehat{ANC}=90^o+90^o=180^o\) \(\Rightarrow\) Tứ giác ANCM nội tiếp \(\Rightarrow\) 4 điểm A, M, C, N cùng thuộc 1 đường tròn. b) Vì AB là đường kính của (O) \(\Rightarrow sđ\stackrel\frown{AB}=180^o\) Mà I là điểm chính giữa của cung AB \(\Rightarrow sđ\stackrel\frown{IA}=\dfrac{sđ\stackrel\frown{AB}}{2}=\dfrac{180^o}{2}=90^o\) Lại có \(\widehat{ANI}\) là góc nội tiếp chắn \(\stackrel\frown{IA}\) \(\Rightarrow\widehat{ANI}=\dfrac{1}{2}sđ\stackrel\frown{IA}=\dfrac{1}{2}.90^o=45^o\) hay \(\widehat{ANM}=45^o\) Mặt khác, tứ giác ANCM nội tiếp \(\Rightarrow\widehat{ANM}=\widehat{ACM}\) Mà \(\widehat{ANM}=45^o\Rightarrow\widehat{ACM}=45^o\) Lại có \(\Delta ACM\) vuông tại M \(\Rightarrow\Delta ACM\) vuông cân tại M \(\Rightarrow AM=CM\) c) Kẻ đường kính ID của (O)  Ta có \(MN=IN-IM\) Mà IN là dây cỏa (O) nên hiển nhiên \(IN\le ID\), nhưng do IN không đi qua O nên \(IN< ID\) (1) Dễ dàng chứng minh \(IO\perp AB\) tại O, do đó \(\Delta IOM\) vuông tại O \(\Rightarrow IM>IO\) (không xảy ra dấu "=" vì M không trùng với O) \(\Rightarrow-IM< -IO\) (2) Từ (1) và (2) \(\Rightarrow IN-IM< ID-IO\Leftrightarrow MN< OD=R\) Vậy ta có đpcm.  

Miug

...

a) Khi \(m=2\) thì \(\left(d\right):y=2x+3\) Phương trình hoành độ giao điểm của (P) và (d) là: \(x^2=2x+3\Leftrightarrow x^2-2x-3=0\) (*) \(\left(a=1;b=-2;c=-3\right)\) Pt (*) có \(a-b+c=1-\left(-2\right)-3=0\) nên pt này có 2 nghiệm: \(x_1=-1;x_2=-\dfrac{-3}{1}=3\) Khi \(x=-1\Rightarrow y=x^2=\left(-1\right)^2=1\) Khi \(x=3\Rightarrow y=x^2=3^2=9\) Vậy tọa độ giao điểm của (P) và (d) khi \(m=2\) là các điểm \(\left(-1;1\right);\left(3;9\right)\) b) Phương trình hoành độ giao điểm của (P) và (d) là \(x^2=mx+3\Leftrightarrow x^2-mx-3=0\) (1) \(\left(a=1;b=-m;c=-3\right)\) pt (*) có \(ac=1.\left(-3\right)=-3< 0\), như vậy pt này luôn có 2 nghiệm phân biệt hay (d) luôn cắt (P) tại 2 điểm phân biệt. Khi đó, áp dụng hệ thức Vi-ét, ta có \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-3\end{matrix}\right.\) Lại có \(y_1=x_1^2;y_2=x_2^2\) Do đó \(y_1+y_2=4\left(x_1+x_2\right)+3\Leftrightarrow x_1^2+x_2^2=4m+3\) \(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=4m+3\Leftrightarrow m^2-2.\left(-3\right)=4m+3\)\(\Leftrightarrow m^2-4m+3=0\) (2) \(\left(a=1;b=-4;c=3\right)\) Pt (2) có \(a+b+c=1-4+3=0\) nên pt này có 2 nghiệm: \(m_1=1;m_2=3\) Vậy để (d) cắt (P) tại 2 điểm có tọa độ thỏa mãn yêu cầu đề bài thì \(\left[{}\begin{matrix}m=1\\m=3\end{matrix}\right.\)    

  

TL \(-\dfrac{3}{4}+x=\dfrac{1}{2}+\dfrac{5}{6}\) \(\Leftrightarrow-\dfrac{3}{4}+x=\dfrac{4}{3}\) \(\Leftrightarrow x=\dfrac{4}{3}-\dfrac{3}{4}\) \(\Rightarrow x=\dfrac{7}{12}\) Hoktot~