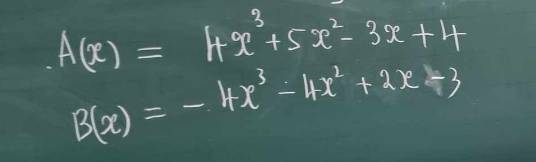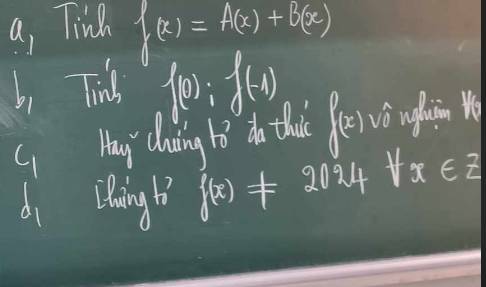Ta có:\(x=100\)

\(\Rightarrow x+1=101\)

\(\Rightarrow M=x^8-\left(x+1\right)x^7+\left(x+1\right)x^6-\left(x+1\right)x^5+...+\left(x+1\right)x^2-\left(x+1\right)x+125\\ \Rightarrow M=x^8-x^8-x^7+x^7+x^6-x^6-x^5+...x^3+x^2-x^2-x+125\\ \Rightarrow M=-x+125\\ \Rightarrow M=-100+125\\ \Rightarrow M=25.\)

 giúp mik câu 12,13,14,15,16,17nha.

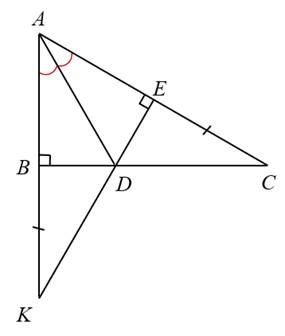
a Xét ΔBAD vuông tại A và ΔEAD vuông tại E có

AD chung

\(\widehat{BAD}=\widehat{EAD}\)

Do đó: ΔBAD=ΔEAD

b: Ta có: ΔABD=ΔAED
=>AB=AE và DB=DE

Ta có: AB=AE
=>A nằm trên đường trung trực của BE(1)

Ta có: DB=DE

=>D nằm trên đường trung trực của BE(2)

Từ (1),(2) suy ra AD là đường trung trực của BE

c: Xét ΔDBK vuông tại B và ΔDEC vuông tại E có

DB=DE

BK=EC

Do đó: ΔDBK=ΔDEC

=>\(\widehat{BDK}=\widehat{EDC}\)

mà \(\widehat{EDC}+\widehat{BDE}=180^0\)(hai góc kề bù)

nên \(\widehat{BDE}+\widehat{BDK}=180^0\)

=>E,D,K thẳng hàng

a) Xét $\Delta BAD$ và $\Delta EAD$:

      ���^=���^=90∘ABD=AED=90∘.

      $AD$ chung.

      ���^=���^(��)BAD=EAD(gt).

Suy ra $\Delta BAD=\Delta EAD$ { (cạnh huyền - góc nhọn)

b) Do $\Delta BAD=\Delta EAD$ (câu a) nên + ) $AB=AE$ (Cặp cạnh tương ứng)

$A$ nằm trên đường trung trực của đoạn thẳng $BE$ (1)

+) $DB=DE$ (Cặp cạnh tương ứng)

$D$ nằm trên đường trung trực của đoạn thẳng $BE$ (2)

Từ (1) và (2) ta suy ra $AD$ là đường trung trực của $BE$.

c) Xét $\Delta BDK$ và $\Delta EDC$:

      ���^=���^KBD=CED.

      $BK=CE$ (gt).

      $BD=DE$.

Suy ra $\Delta BDK=\Delta EDC$ (c.g.c)

Suy ra ���^=���^BDK=EDC (Cặp góc tương ứng) (1)

Mặt khác ta có $D$ thuộc cạnh $BC$ nên ���^+���^=180∘EDC+EDB=180∘. (2)

v

Từ (1) và (2) suy ra ���^+���^=180∘BDK+EDB=180∘.

Hay ba điểm $E,D,K$ thẳng hàng.

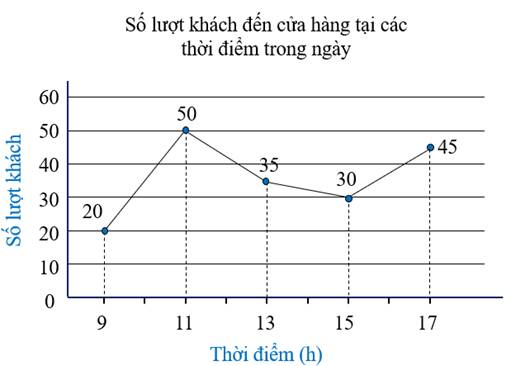
a) Cửa hàng đông khách nhất vào thời điểm 11 giờ

Cửa hàng vắng khách nhất vào thời điểm 9 giờ.

b) Số lượt khách đến cửa hàng từ 15 giờ đến 17 giờ tăng 15 lượt khách.

a) Cửa hàng đông khách nhất vào thời điểm 11 giờ

Cửa hàng vắng khách nhất vào thời điểm 9 giờ.

b) Số lượt khách đến cửa hàng từ 15 giờ đến 17 giờ tăng 15 lượt khách.

đây ạ

2. 

a) Cửa hàng đông khách nhất vào thời điểm 11 giờ

Cửa hàng vắng khách nhất vào thời điểm 9 giờ.

b) Số lượt khách đến cửa hàng từ 15 giờ đến 17 giờ tăng 15 lượt khách.

2. 

a) Cửa hàng đông khách nhất vào thời điểm 11 giờ

Cửa hàng vắng khách nhất vào thời điểm 9 giờ.

b) Số lượt khách đến cửa hàng từ 15 giờ đến 17 giờ tăng 15 lượt khách.

      Câu 3: 

      Giải

Chiều cao của hình hộp chữ nhật là: 6,9 x \(\dfrac{2}{3}\) = 4,6

Thể tích của hình hộp chữ nhật là: 6,9 x 5,2 x 4,6 = 165,048 (cm³)

Đáp số: 165,048 cm³

Câu 4:

        Giải:

Chiều cao của hình thang là:

      38,5 x  \(\dfrac{2}{5}\) = \(\dfrac{77}{5}\) (m)

Diện tích mảnh vườn đó là:

     (38,5 + 29) x \(\dfrac{77}{5}\) : 2 = 519,75 (m²)

Đáp số: 519,75 m²

a: f(x)=A(x)+B(x)

\(=4x^3+5x^2-3x+4-4x^3-4x^2+2x-3\)

\(=x^2-x+1\)

b: \(f\left(0\right)=0^2-0+1=1\)

\(f\left(1\right)=1^2-1+1=1\)

c: Đặt f(x)=0

=>\(x^2-x+1=0\)

=>\(x^2-x+\dfrac{1}{4}+\dfrac{3}{4}=0\)

=>\(\left(x-\dfrac{1}{2}\right)^2+\dfrac{3}{4}=0\)(vô lý)

=>f(x) không có nghiệm

c: Đặt f(x)=2024

=>\(x^2-x+1=2024\)

=>\(x^2-x-2023=0\)(1)

\(\text{Δ}=\left(-1\right)^2-4\cdot1\cdot\left(-2023\right)=8093>0\)

Do đó: Phương trình (1) có hai nghiệm phân biệt là:

\(\left\{{}\begin{matrix}x_1=\dfrac{1-\sqrt{8093}}{2}\notin Z\\x_2=\dfrac{1+\sqrt{8093}}{2}\notin Z\end{matrix}\right.\)

=>f(x) luôn khác 2024 với mọi số nguyên x

Thay x=-2 và y=2 vào M, ta được:

\(M=2\cdot\left(-2\right)\cdot2-4\cdot\left(-2\right)+5\)

=-8+8+5

=5