(x-1)^2+(y+1)^2=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(2xy+x-y+xy^2+2xy\)
\(=x-y+xy^2+\left(2xy+2xy\right)\)
\(=x-y+xy^2+4xy\)
b: \(5xy^2+4y-4x\cdot2y^2\)
\(=4y+5xy^2-8xy^2\)
\(=4x-3xy^2\)
c: \(\sqrt{25}+\sqrt{36}+\sqrt{49}+...+\sqrt{100}\)
=5+6+7+8+9+10
=15+15+15
=45
d: Đặt \(A=1+4+9+16+...+9801+10000\)
Đặt \(B=1+8+27+...+729+1000\)
\(A=1+4+9+...+10000\)
\(=1^2+2^2+...+100^2\)
\(=\dfrac{100\left(100+1\right)\left(2\cdot100+1\right)}{6}\)
\(=\dfrac{100\cdot101\cdot201}{6}\)
\(B=1+8+27+...+1000\)
\(=1^3+2^3+...+10^3=\left(1+2+...+10\right)^2\)
\(=55^2\)
=>\(A-B=\dfrac{100\cdot101\cdot201}{6}-55^2=335325\)

\(\dfrac{A+C+E}{3}\) + \(\dfrac{A+B+D}{3}\) = 40 + 28
\(\dfrac{2A}{3}\)+\(\dfrac{B+C+E+D}{3}\)= 68
\(\dfrac{2A}{3}\)+ 33 = 68
\(\dfrac{2A}{3}\)=35
2A = 35 X 3
2A = 105
A =\(\dfrac{105}{2}\)
Từ (1) \(\Rightarrow A+C+E=40\cdot3=120\)
Từ (2) \(\Rightarrow A+B+D=28\cdot3=84\)
Từ (3) \(\Rightarrow B+C+D+E=33\cdot3=99\)
Suy ra:
\(\left(A+C+E+A+B+D\right)-\left(B+C+D+E\right)=\left(120+84\right)-99\)
\(2A+\left(B+C+D+E\right)-\left(B+C+D+E\right)=105\)
\(2A=105\)
\(A=52,5\)
Vậy \(A=52,5\)

b: \(\dfrac{1}{2^2}< \dfrac{1}{1\cdot2}=1-\dfrac{1}{2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{2\cdot3}=\dfrac{1}{2}-\dfrac{1}{3}\)
...
\(\dfrac{1}{100^2}< \dfrac{1}{99}-\dfrac{1}{100}\)
Do đó: \(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+...+\dfrac{1}{100^2}< 1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
=>\(A< 1-\dfrac{1}{100}\)
=>A<1
=>0<A<1
=>A không là số tự nhiên
a: \(A=1+4+9+...+10000\)
\(=1^2+2^2+...+100^2\)
\(=\dfrac{100\left(100+1\right)\left(2\cdot100+1\right)}{6}\)
\(=\dfrac{100\cdot101\cdot201}{6}\)
\(B=1+8+27+...+1000\)
\(=1^3+2^3+...+10^3=\left(1+2+...+10\right)^2\)
\(=55^2\)
=>\(A-B=\dfrac{100\cdot101\cdot201}{6}-55^2=335325\)

A = 12 + 22 + 32 + ... + 1002
A = 1 + 2 x (1 + 1) + 3 x (2 + 1) + ... + 100 x (99 + 1)
A = 1 + 2 x 1 + 2 + 3 x 2 + 3 + ... + 100 x 99 + 100
A = (1 + 2 + 3 + ... + 100) + (1 x 2 + 2 x 3 + 3 x 4 + ... + 99 x 100)
Ta gọi biểu thức: 1 + 2 + 3 + ... + 100 = C
1 x 2 + 2 x 3 + 3 x 4 + ... + 99 x 100 = D
C = (1 + 100) x 100 : 2 = 5 050
D = 1 x 2 + 2 x 3 + 3 x 4 + ... + 99 x 100
3D = 1 x 2 x 3 + 2 x 3 x 3 + 3 x 4 x 3 + ... + 99 x 100 x 3
3D = 1 x 2 x 3 + 2 x 3 x (4 - 1) +...+ 99 x 100 x (101 - 98)
3D = 1 x 2 x 3 + 2 x 3 x 4 - 2 x 3 x 1 +... - 99 x 100 x 98
3D = 98 x 99 x 100
3D = 970 200
D = 970 200 : 3
D = 323 400
A = 5 050 + 323 400 = 328 450
B = 13 + 23 + 33 + ... + 503
B = 1 + 2 x ( 22) + 3 x (32) + ... + 50 x (502)
B = 1 + 22 x (1 + 1) + 32 x (2 + 1) + ... + 502 x (49 + 1)
B = 12 + 1 x 22 + 22 + 2 x 32 + 32 + ... + 49 x 502 + 502
B = (12 + 22 + 32 + ... + 502) + (1 x 22 + 2 x 32 + ... + 49 x 502)
Đặt biểu thức: 12 + 22 + 32 + ... + 502 = E
E = 1 + 2 x (1 + 1) + 3 x (2 + 1) + ... + 50 x (49 + 1)
E = 1 + 1 x 2 + 2 + 3 x 2 + 3 + ... + 50 x 49 + 50
E = (1 + 2 + 3 + ... + 50) + (1 x 2 + 2 x 3 + ... + 49 x 50)
Đặt biểu thức: 1 + 2 + 3 + ... + 50 = F
1 x 2 + 2 x 3 + ... + 49 x 50 = G
F = (1 + 50) x 50 : 2 = 1275
3G = 1 x 2 x 3 + 2 x 3 x 3 + ... + 49 x 50 x 3
3G = 1 x 2 x 3 + 2 x 3 x (4 - 1) + ... + 49 x 50 x (51 - 48)
3G = 1 x 2 x 3 + 2 x 3 x 4 - 2 x 3 x 1 + ... + 49 x 50 x 51 - 49 x 50 x 48
3G = 49 x 50 x 51
3G = 124950
G = 124950 : 3 = 41650
B = 41650 + 1275 = 42925
b) B = 3 + 32 + 33 + 34 + ... + 3100
3B = 32 + 33 + 34 + ... + 3101
3B - B = 3101 - 3
2B = 3101 - 3
Ta có:
2B + 3n = 3101
3101 - 3 + 3n = 3101
⇒ 3n = 3
31 = 3
⇒ n = 1
b: \(B=3+3^2+...+3^{100}\)
=>\(3B=3^2+3^3+...+3^{101}\)
=>\(3B-B=3^2+3^3+...+3^{101}-3-3^2-...-3^{100}\)
=>\(2B=3^{101}-3\)
\(2B+3^n=3^{101}\)
=>\(3^{101}-3+3^n=3^{101}\)
=>\(3^n=3\)
=>n=1

x:y:z=1:2:3
=>\(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{3}\)
mà 2x+6y+2z=60
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{3}=\dfrac{2x+6y+2z}{2\cdot1+6\cdot2+2\cdot3}=\dfrac{60}{20}=3\)
=>\(x=3\cdot1=3;y=3\cdot2=6;z=3\cdot3=9\)
Ta có: \(\dfrac{x}{1}=\dfrac{y}{2}=\dfrac{z}{3}\Rightarrow\dfrac{2x}{2}=\dfrac{6y}{12}=\dfrac{2z}{6}\)
Áp dụng tính chất dãy tỉ sống bằng nhau, ta có:
\(\dfrac{2x}{2}=\dfrac{6y}{12}=\dfrac{2z}{6}=\dfrac{2x+6y+2z}{2+12+6}=\dfrac{60}{20}=3\)
Do đó:
\(\dfrac{x}{1}=3\Rightarrow x=1.3=3\)
\(\dfrac{y}{2}=3\Rightarrow y=2.3=6\)
\(\dfrac{z}{3}=3\Rightarrow z=3.3=9\)
Vậy x = 3; y = 6; z = 9.
\(#NqHahh\)

Olm chào em, em cần gõ phân số trên olm thì em chọn biểu tượng \(\Sigma\) góc trái màn hình sau đó chọn biểu tượng phân số rồi chèn phân số em nhé. Cảm ơn em đã đồng hành cùng Olm. Chúc em học tập hiệu quả cùng Olm.vn
Nguyễn Thị Thương Hoài : vâng ạ, em hiểu rồi, em cam ơn cô ạ☺

\(\left(1+2+3+...+100\right)\cdot\left(\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{1}{6}+\dfrac{1}{8}\right)\cdot\dfrac{\left(1+8+27+64+125+216+343\right)}{1+4+9+16+25+36+49}\)
\(=100\cdot\dfrac{101}{2}\cdot\left(\dfrac{12}{24}+\dfrac{6}{24}+\dfrac{4}{24}+\dfrac{3}{24}\right)\cdot\dfrac{\left(1+2+3+4+5+6+7\right)^2}{140}\)
\(=101\cdot50\cdot\dfrac{25}{24}\cdot\dfrac{784}{140}\)
\(=5050\cdot\dfrac{35}{6}=\dfrac{88375}{3}\)

\(\dfrac{11}{15}-\dfrac{9}{10}< x< \dfrac{11}{15}:\dfrac{9}{10}\)
=>\(\dfrac{22}{30}-\dfrac{27}{30}< x< \dfrac{11}{15}\cdot\dfrac{10}{9}\)
=>\(-\dfrac{5}{30}< x< \dfrac{22}{27}\)
mà x nguyên
nên x=0
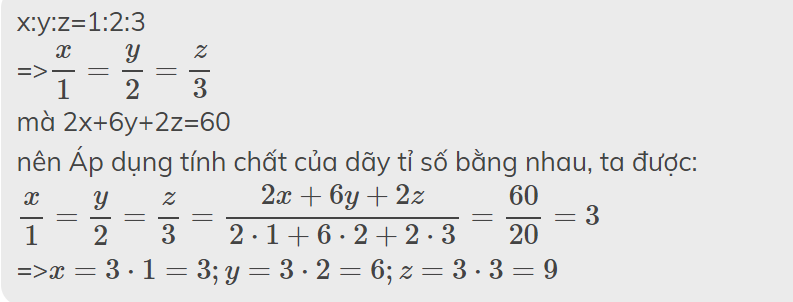
\(\left(x-1\right)^2+\left(y+1\right)^2=0\)
Nhận xét:
\(\left\{{}\begin{matrix}\left(x-1\right)^2\ge0\\\left(y+1\right)^2\ge0\end{matrix}\right.\)
\(\Rightarrow\left(x-1\right)^2+\left(y+1\right)^2\ge0\)
Do đó: Dấu "=" xảy ra khi:
\(\left\{{}\begin{matrix}x-1=0\\y+1=0\end{matrix}\right.\)
\(\Rightarrow x=1;y=-1\)
Vậy \(x=1;y=-1\)