Ta có:

\(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\\ 2A=2.\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2021}}+\dfrac{2}{2^{2022}}\right)\\ 2A=1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2020}}-\dfrac{1}{2^{2021}}\\ 2A-A=\left(1+\dfrac{1}{2}+\dfrac{1}{2^2}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\right)-\left(\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2021}}+\dfrac{1}{2^{2022}}\right)\\ A=1-\dfrac{1}{2^{2022}}\\ \Rightarrow A< 1\)

\(B=\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{17}{60}\\ B=\dfrac{16}{15}\\ \Rightarrow B>1\)

Vì A<1 mà B>1 ⇒ A<1<B⇒A<B

Vậy A<B.

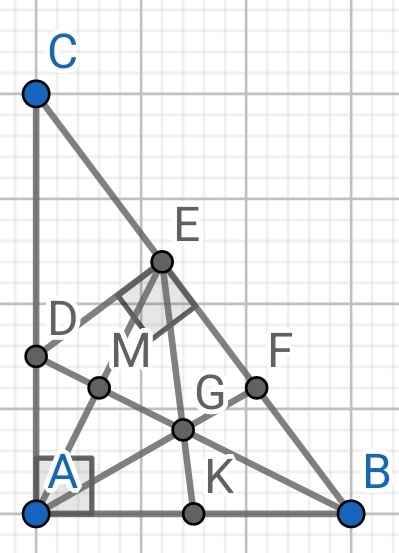
a) Do BD là tia phân giác của ∠ABC (gt)

⇒ ∠ABD = ∠CBD

⇒ ∠ABD = ∠EBD

Xét hai tam giác vuông: ∆ABD và ∆EBD có:

BD là cạnh chung

∠ABD = ∠EBD (cmt)

⇒ ∆ABD = ∆EBD (cạnh huyền - góc nhọn)

b) Do ∆ABD = ∆EBD (cmt)

⇒ AB = EB (hai cạnh tương ứng)

⇒ B nằm trên đường trung trực của AE (1)

Do ∆ABD = ∆EBD (cmt)

⇒ AD = ED (hai cạnh tương ứng)

⇒ D nằm trên đường trung trực của AE (2)

Từ (1) và (2) ⇒ BD là đường trung trực của AE

Mà M là giao điểm của BD và AE (gt)

⇒ M là trung điểm của AE

c) Do F là trung điểm của BE (gt)

⇒ BF = BE : 2

Mà BE = AB (cmt)

⇒ BF = AB : 2

Mà BF = BK (gt)

⇒ BK = AB : 2

⇒ K là trung điểm của AB

∆ABE có:

BM là đường trung tuyến (do M là trung điểm của AE)

AF là đường trung tuyến (do F là trung điểm của BE)

Mà G là giao điểm của BM và AF (gt)

⇒ EG là đường trung tuyến thứ ba

Mà K là trung điểm của AB (cmt)

⇒ E, G, K thẳng hàng

I K Q O P H

Xét (O) có

sđ cung IQ = sđ cung KQ (gt)

=> IQ=KQ => tg IQK cân tại Q

OI=OK (bán kính (O))

\(\Rightarrow OQ\perp IK\) (trong tam giác cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao)

\(\Rightarrow\widehat{QOK}=90^o\)

Ta có

\(\widehat{IPK}=90^o\) (góc nội tiếp chắn nửa đường tròn)

=> O và P cùng nhìn HK dưới 2 góc bằng nhau và bằng 90 độ

=> O và P thuộc đường tròn đường kính HK => OKPH là tứ giác nội tiếp

b/

Xét tg HIK có

\(OH\perp IK;OI=OK\) => tg HIK cân tại H (tam giác có đường cao đồng thời là đường trung tuyến thì đó là tg cân)

\(\Rightarrow\widehat{KIP}=\widehat{HKI}\) (góc ở đáy tg cân)

Ta có

\(\widehat{PHK}=\widehat{KIP}+\widehat{HKI}\) (trong tg góc ngoài bằng tổng 2 góc trong không kề với nó)

\(\Rightarrow\widehat{PHK}=2\widehat{KIP}\Rightarrow\widehat{KIP}=\dfrac{1}{2}\widehat{PHK}\)

a) A(x) = -2x² + x⁴ - 7x + x⁴ + 7

= (x⁴ + x⁴) - 2x² - 7x + 7

= 2x⁴ - 2x² - 7x + 7

B(x) = x⁴ + 2x - 3x⁴ - 6 + 2x² - 4

= (x⁴ - 3x⁴) + 2x² + 2x + (-6 - 4)

= -2x⁴ + 2x² + 2x - 10

b) A(x) + B(x)

= (2x⁴ - 2x² - 7x + 7) + (-2x⁴ + 2x² + 2x - 10)

= 2x⁴ - 2x² - 7x + 7 - 2x⁴ + 2x² + 2x - 10

= (2x⁴ - 2x⁴) + (-2x² + 2x²) + (-7x + 2x) + (7 - 10)

= -5x - 3

A(x) - B(x) = (2x⁴ - 2x² - 7x + 7) - (-2x⁴ + 2x² + 2x - 10)

= 2x⁴ - 2x² - 7x + 7 + 2x⁴ - 2x² - 2x + 10

= (2x⁴ + 2x⁴) + (-2x² - 2x²) + (-7x - 2x) + (7 + 10)

= 4x⁴ - 4x² - 9x + 17

c) C(x) = A(x) + B(x) = -5x - 3

Cho C(x) = 0

-5x - 3 = 0

5x = -3

x = -3/5

Vậy nghiệm của đa thức C(x) là x = -3/5

d) D(x) = C(x).(2x² - 4x + 2)

= (-5x - 3)(2x² - 4x + 2)

= -5x(2x² - 4x + 2) - 3(2x² - 4x + 2)

= -10x³ + 20x² - 10x - 6x² + 12x - 6

= -10x³ + (20x² - 6x²) + (-10x + 12x) - 6

= -10x³ + 14x² + 2x - 6

Vì N nằm giữa P và Q nên:

PN+NQ=PQ

       NQ=PQ-PN

             =10-3=7(cm)

Vì I là trung điểm cuả NQ nên:

NI=IQ=1/2NQ=1/2.7=3,5(cm) 

                    Đáp số:NQ=3,5cm

Vì N nằm giữa P và Q nên:

PN+NQ=PQ

       NQ=PQ-PN

             =10-3=7(cm)

Vì I là trung điểm cuả NQ nên:

NI=IQ=1/2NQ=1/2.7=3,5(cm) 

                    Đáp số:NQ=3,5cm

               Giải:

Số sách tham khảo là: 300 x \(\dfrac{7}{20}\) = 105 (quyển)

Số sách truyện là: 300 x 25 : 100 = 75 (quyển)

Số sách khoa học và đời sống là: 300 -  105  - 75  = 120 (quyển)

Kết luận:...

Số sách tham khảo là:

   300 \(.\) \(\dfrac{7}{20}\) = 105 (quyển)

Số truyện là:

   300 \(.\) 25% = 75 (quyển)

Số sách khoa học và đời sống là:

   300 - (105 + 75) = 120 (quyển)

C=4048.(1-\(\dfrac{1}{2}\)).(1-\(\dfrac{1}{3}\)).(-\(\dfrac{1}{4}\)).....(1-\(\dfrac{1}{2024}\))

C=4048.\(\dfrac{1}{2}\).\(\dfrac{2}{3}\).\(\dfrac{3}{4}\).....\(\dfrac{2023}{2024}\)

C=4048.\(\dfrac{1.2.3.....2023}{2.3.4.....2024}\)

C=4048.\(\dfrac{1}{2024}\)

C=2

C = 4048 \(.\) (1 - \(\dfrac{1}{2}\)) (1 - \(\dfrac{1}{3}\)) (1 - \(\dfrac{1}{4}\)).....(1 - \(\dfrac{1}{2024}\))

C = 4048 \(.\) \(\dfrac{1}{2}\) \(.\) \(\dfrac{2}{3}\) \(.\) \(\dfrac{3}{4}\)......\(\dfrac{2023}{2024}\)

C = 4048 \(.\) \(\dfrac{1.2.3....2023}{2.3.4....2024}\)

C = 4048 \(.\) \(\dfrac{1}{2024}\)

C = 2

a; A = 17 x (\(\dfrac{1313}{5151}\) + \(\dfrac{1111}{3434}\)) : \(\dfrac{177}{12}\)

   A = 17 x (\(\dfrac{13}{51}\) + \(\dfrac{11}{34}\)) : \(\dfrac{177}{22}\)

  A = 17 x \(\dfrac{59}{102}\) : \(\dfrac{177}{12}\)

A = \(\dfrac{59}{6}\) : \(\dfrac{177}{12}\)

A = \(\dfrac{2}{3}\)

`#3107.101107`

`a)`

`A = 17 \times (1313/5151 + 1111/3434) \div 177/12`

`= 17 \times (13/51 + 11/34) \div 177/12`

`= 17 \times 59/102 \times 12/177`

`= (17 \times 12/177) \times 59/102`

`= 68/59 \times 59/102`

`= 68/102 = 2/3`

Vậy, `A = 2/3`

`b)`

`B = 3/5 + 47/13 - 25/8 + 1/8 - 8/13 + 2/5`

`= (3/5 + 2/5) + (-25/8 + 1/8) + (47/13 - 8/13)`

`= 5/5 + (-24/8) + 39/13`

`= 1 - 3 + 3 = 1`

Vậy, `B = 1.`

`B =