Ta thấy 1 cặp tam giác đồng dạng quen thuộc là \(\Delta HAB~\Delta HCA\), từ đó suy ra \(\dfrac{S_{HAB}}{S_{HCA}}=\left(\dfrac{AB}{AC}\right)^2\). Mà ta lại có \(\dfrac{S_{HAB}}{S_{HCA}}=\dfrac{HB}{HC}\) (2 tam giác có chung đường cao hạ từ A) nên suy ra đpcm.

\(\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+\sqrt{12}+\sqrt{18-\sqrt{128}}}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+2\sqrt{3}+\sqrt{4^2-2.4.\sqrt{2}+\sqrt{2^2}}}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+2\sqrt{3}+\sqrt{\left(4-\sqrt{2}\right)^2}}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+2\sqrt{3}+\left|4-\sqrt{2}\right|}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\sqrt{2}+2\sqrt{3}+4-\sqrt{2}}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{4+2\sqrt{3}}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{\left(\sqrt{3}+1\right)^2}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{3-\sqrt{3}-1}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{2}\sqrt{2-\sqrt{3}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{4-2\sqrt{3}}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{\left(\sqrt{3}-1\right)^2}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\left|\sqrt{3}-1\right|}\)

\(=\left(\sqrt{3}-1\right)\sqrt{6+2\sqrt{3}-2}\)

\(=\left(\sqrt{3}-1\right)\sqrt{4+2\sqrt{3}}\)

\(=\left(\sqrt{3}-1\right)\sqrt{\left(\sqrt{3}+1\right)^2}\)

\(=\left(\sqrt{3}-1\right)\left(\sqrt{3}+1\right)\)

\(=\sqrt{3^2}-1^2\\ =3-1\\ =2\)

\(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}\)

\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{\left(2+\sqrt{3}\right)^2}}}}\)

\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\left|2+\sqrt{3}\right|}}}\)

\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{3}-20}}}\)

\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)

\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{5^2-2.5.\sqrt{3}+\sqrt{3^2}}}}\)

\(=\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)

\(=\sqrt{4+\sqrt{5\sqrt{3}+5\left|5-\sqrt{3}\right|}}\)

\(=\sqrt{4+\sqrt{5\sqrt{3}+25-5\sqrt{3}}}\)

\(=\sqrt{4+\sqrt{25}}\)

\(=\sqrt{4+5}\)

\(=\sqrt{9}\\ =3\)

 \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{7+4\sqrt{3}}}}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10\sqrt{\left(2+\sqrt{3}\right)^2}}}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10.|2+\sqrt{3}|}}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-10.\left(2+\sqrt{3}\right)}}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{48-20-10\sqrt{3}}}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{28-10\sqrt{3}}}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+5\sqrt{\left(5-\sqrt{3}\right)^2}}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+5.|5-\sqrt{3}|}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+5.\left(5-\sqrt{3}\right)}}\)

= \(\sqrt{4+\sqrt{5\sqrt{3}+25-5\sqrt{3}}}\)

= \(\sqrt{4+\sqrt{25}}\)

= \(\sqrt{4+5}\)

= \(\sqrt{9}\)

= \(3\)

\(e,\dfrac{\sqrt{4x-1}}{\sqrt{7-2x}-2}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}4x-1\ge0\\7-2x\ne4\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{4}\\x\ne-\dfrac{3}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{4}\)

\(d,\dfrac{\sqrt{2x-1}}{\sqrt{2x+17}+1}\) có nghĩa \(\Leftrightarrow\left[{}\begin{matrix}2x-1\ge0\\2x+17\ge0\end{matrix}\right.\)  \(\Leftrightarrow\left[{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ge-\dfrac{17}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ge\dfrac{1}{2}\)

 \(b,c,\dfrac{3}{\sqrt{2x-17}}\) có nghĩa \(\Leftrightarrow2x-17>0\Leftrightarrow x>\dfrac{17}{2}\)

\(a,\sqrt{2-5x}\) có nghĩa \(\Leftrightarrow2-5x\ge0\Leftrightarrow x\le\dfrac{2}{5}\)

Hạ đường cao AH của tam giác ABD => AH=14,4cm

Pytago => AD^2-AH^2=DH^2

            => DH^2=116,64

            => DH=10,8cm

HT lượng => HA^2=HB.HC

                => HB=HA^2/HB=14,4^2/10,8=19,2cm

=> BD=HD+HB=10,8+19,2=30m

Pytago => AB^2=AH^2+HB^2=576

            => AB=24cm

=> chu vi HCN ABCD là: 2(AB+AD)=2(18+24)=84(cm^2)

Ta có:

\(AH^2=BH.HC\Rightarrow HC=\dfrac{AH^2}{BH}=\dfrac{3^2}{4}=\dfrac{9}{4}\left(cm\right)\)

\(BC=BH+HC=4+\dfrac{9}{4}=9\left(cm\right)\)

\(AB=\sqrt{BH.BC}=\sqrt{4.9}=6\left(cm\right)\)

\(AC=\sqrt{CH.BC}=\sqrt{\dfrac{9}{4}.9}=\dfrac{9}{2}\left(cm\right)\)

1 do

2 was traveling

3 was driving

4  read - has become

5 has loved - was

6 has eaten

7  have done

8 have cleaned

9 was watching

10 saw

#\(Errink \times Cream\)

#\(yGLinh\)

1. do

2. was traveling

3. was driving

4.  read - has become

5. has loved - was

6. has eaten

7.  have done

8. have cleaned

9. was watching

10. saw

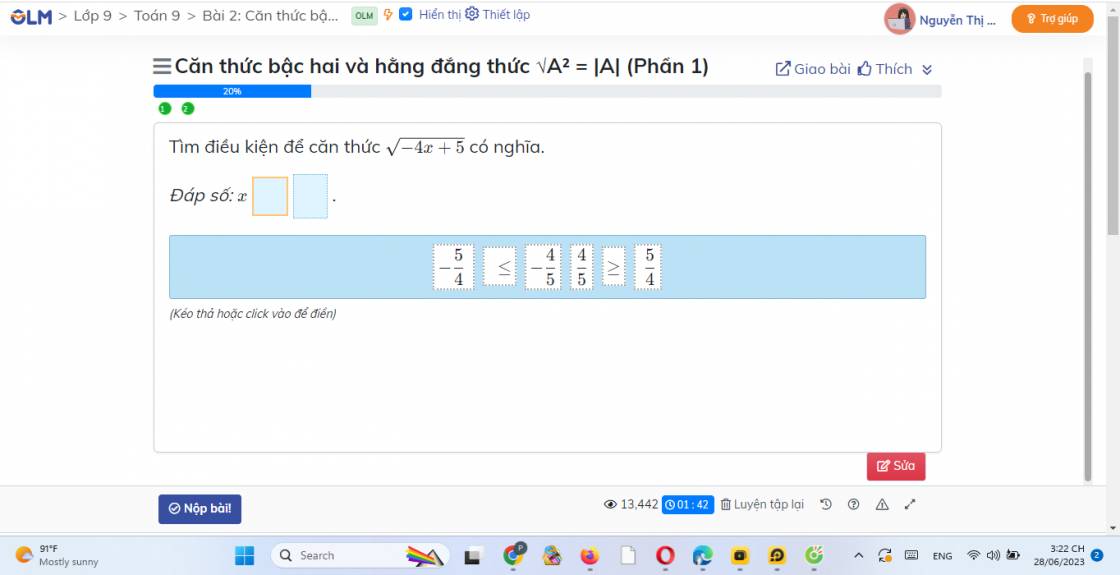
Câu c của em đấy nhé: \(\sqrt{-4x+5}\) có nghĩa ⇔ -4\(x\) + 5 ≥ 0 

                                                                                   4\(x\) ≤ 5 

                                                                                    \(x\) ≤ \(\dfrac{5}{4}\) 

Vậy em kéo dấu ≤ vào ô trống thứ nhất, sau đó em kéo \(\dfrac{5}{4}\) vào ô trống thứ hai rồi ấn nút nộp bài là xong em nhé

Aabb có TLGT là 1Ab:1ab

Nếu Aabb x kiểu gen chỉ cho 1 giao tử duy nhất sẽ cho mô hình phân li kiểu hình 1:1 

VD: Aabb x aabb hay Aabb x aaBB