Cho x>0; y>0 và 2x+3y\(\le\) 2. Tìm GTNN của \(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(\left(\sqrt{a}-\sqrt{b}\right)^2\ge0\Leftrightarrow a-2\sqrt{ab}+b\ge0\Leftrightarrow a+b\ge2\sqrt{ab}\)
Dấu \(=\)khi \(a=b\ge0\).
Tương tự ta cũng có: \(b+c\ge2\sqrt{bc},c+a\ge2\sqrt{ca}\).
Cộng lại vế theo vế ta được:
\(2\left(a+b+c\right)\ge2\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\right)\)
\(\Leftrightarrow a+b+c\ge\sqrt{ab}+\sqrt{bc}+\sqrt{ca}\)
Dấu \(=\)khi \(a=b=c\).

sửa đề : \(E=\left(\frac{\sqrt{x}}{\sqrt{x}-1}-\frac{1}{x-\sqrt{x}}\right):\left(\frac{1}{\sqrt{x}+1}+\frac{2}{x-1}\right)\)ĐK : \(x>0;x\ne1\)
\(=\left(\frac{x-1}{\sqrt{x}\left(\sqrt{x}-1\right)}\right):\left(\frac{\sqrt{x}+1}{x-1}\right)\)
\(=\frac{\left(x-1\right)^2}{\sqrt{x}\left(x-1\right)}=\frac{x-1}{\sqrt{x}}\)


\(f\left(x\right)=x^2-\left(2m-1\right)x+m^2-m-6=0\)
\(\Delta=\left(2m-1\right)^2-4\left(m^2-m-6\right)>0\)
Suy ra phương trình luôn có hai nghiệm phân biệt
Để \(-5< x_1< x_2< 5\) thì :
\(\hept{\begin{cases}f\left(-5\right)>0\\f\left(5\right)>0\\-5< \frac{2m-1}{2}< 5\end{cases}}\Leftrightarrow\hept{\begin{cases}m^2+9m+14>0\\m^2-11m+24>0\\-\frac{9}{2}< m< \frac{11}{2}\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x< -7\left(h\right)x>-2\\x< 3\left(h\right)x>8\\-\frac{9}{2}< m< \frac{11}{2}\end{cases}}\Leftrightarrow-2< x< 3\)
Chữa:
\(\hept{\begin{cases}m< -7\left(h\right)m>-2\\m< 3\left(h\right)m>8\\-\frac{9}{2}< m< \frac{11}{2}\end{cases}}\Leftrightarrow-2< m< 3\)

a) \(\sqrt{15}< \sqrt{16}=4\)
\(\sqrt{2}< \sqrt{4}=2\)
\(\Rightarrow\sqrt{15}+\sqrt{2}< \sqrt{16}+\sqrt{4}=4+2=6\)
\(\sqrt{14}< \sqrt{16}=4\)
\(\sqrt{3}< \sqrt{9}=3\)
\(\Rightarrow\sqrt{14}+\sqrt{3}< \sqrt{16}+\sqrt{9}=4+3=7\)
\(\Leftrightarrow\sqrt{15}+\sqrt{2}< \sqrt{14}+\sqrt{3}\)( nhận thấy 6 < 7)
b) \(\sqrt{29}-\sqrt{28}=\frac{29-28}{\sqrt{29}+\sqrt{28}}=\frac{1}{\sqrt{29}+\sqrt{28}}\)
\(\sqrt{28}-\sqrt{27}=\frac{28-27}{\sqrt{28}+\sqrt{27}}=\frac{1}{\sqrt{28}+\sqrt{27}}\)
Mà \(\sqrt{29}+\sqrt{28}>\sqrt{28}+\sqrt{27}\)
\(\Rightarrow\frac{1}{\sqrt{29}+\sqrt{28}}< \frac{1}{\sqrt{28}+\sqrt{27}}\)
\(\Rightarrow\sqrt{29}-\sqrt{28}< \sqrt{28}-\sqrt{27}\)

giả sử biểu thức là số hữu tỉ thì ta có \(\sqrt{2}+\sqrt{3}=\frac{p}{q}\)
\(\frac{p^2}{q^2}=2+2\sqrt{6}+3\)
\(\frac{p^2}{q^2}-5=2\sqrt{6}\)(ktm)
vì \(\frac{p^2}{q^2}-5\)là số hữu tỉ \(2\sqrt{6}\)là vô tỉ
<=> \(\sqrt{2}+\sqrt{3}\)là số vô tỉ
Giải thích các bước giải:
Gọi x= căn 2 + căn 3
Giả sử x là số hữu tỉ, có nghĩa là x=p/q tối giản (p,q thuộc N, q khác 0).
Ta có: p/q = căn 2 + căn 3
<=> p^2/q^2 = (căn 2 + căn 3)^2
<=> p^2/q^2 = 2 + 2 căn 6 + 3
<=> p^2/q^2 -5 = 2 căn 6 (vô lí)
Vì p^2/q^2 -5 là số hữu tỉ & 2 căn 6 là số vô tỉ.
Vậy x= căn 2 + căn 3 không phải là số hữu tỉ.
=> x= căn 2 + căn 3 là số vô tỉ.


\(\frac{2\left(\sqrt{7}-2\sqrt{3}\right)}{3\sqrt{5}\left(\sqrt{7}-2\sqrt{3}\right)}\)
\(\frac{2}{3\sqrt{5}}\)

Ta có
\(\left(2x+1\right)^2\ge0\forall x\)
\(\left(2x+1\right)^2+9\ge9\)
\(\sqrt{\left(2x+1\right)^2+9}\ge3\)
Dấu = xảy ra
\(\Leftrightarrow2x+1=0\)
\(x=-\frac{1}{2}\)
Vậy min = 3 khi và chỉ khi x = -1/2
 Nhãn
Nhãn
\(2\ge2x+3y\ge2\sqrt{2x.3y}\Rightarrow xy\le\frac{1}{6}.\)
\(A=\frac{4}{4x^2+9y^2}+\frac{9}{xy}=\frac{4}{4x^2+9y^2}+\frac{4}{12xy}+\frac{26}{3xy}\ge\frac{\left(2+2\right)^2}{4x^2+9y^2+12xy}+\frac{26}{3xy}\)
\(\ge\frac{4^2}{2^2}+\frac{26}{3.\frac{1}{6}}=56\)
Dấu \(=\)khi \(\hept{\begin{cases}\frac{2}{4x^2+9y^2}=\frac{2}{12xy}\\2x=3y=1\end{cases}}\Leftrightarrow\hept{\begin{cases}x=\frac{1}{2}\\y=\frac{1}{3}\end{cases}}\)
Áp dụng bất đẳng thức Cô – si cho hai số dương, ta có: 2x + 3y ≥ 2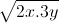
⇔ 2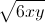 ≤ 2x + 3y
≤ 2x + 3y
Mà 2x + 3y ≤ 2
Do đó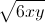 ≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
≤ 1 6xy ≤ 1. Kết hợp kết quả ở câu 1 ta có:
A =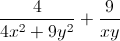 = 4(
= 4(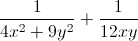 ) +
) + 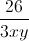 ≥ 4
≥ 4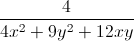 +
+ 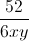 = 16
= 16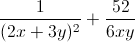 ≥ 16.
≥ 16.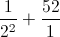 = 56
= 56
Dấu “ = “ xảy ra ⇔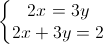 ⇔
⇔ 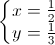
Vậy giá trị nhỏ nhất của biểu thức A là 56.