(x² + y²)² = (x² + y²)(x² + y²)

= x⁴ + x²y² + x²y² + y⁴

= x⁴ + y⁴ + 2x²y² ≥ x⁴ + y⁴

Em xem lại đề nhé!

Cộng 2 lũy thừa cùng số mũ và khác cơ số thì không có công thức chung nào em nhé.

\(\dfrac{x}{5}=\dfrac{y}{3}=\dfrac{z}{2}\) và \(x-3y=20\)

Áp dụng tính chất dãy tỉ số bằng nhau ta có :

\(\dfrac{x}{5}=\dfrac{3y}{9}=\dfrac{z}{2}=\dfrac{x-3y}{5-9}=\dfrac{20}{-4}=-5\)

\(\Rightarrow\left\{{}\begin{matrix}\dfrac{x}{5}=-5< =>x=-25\\\dfrac{y}{3}=-5< =>y=-15\\\dfrac{z}{2}=-5< =>z=-10\end{matrix}\right.\)

Vậy ....

Ta có: \(\left\{{}\begin{matrix}\left|0,25x-1\right|\ge0\forall x\\\left|3-2y\right|\ge0\forall y\end{matrix}\right.\)

\(\Rightarrow\left|0,25x-1\right|+\left|3-2y\right|\ge0\forall x,y\)

Mà: \(\left|0,25x-1\right|+\left|3-2y\right|=0\)

nên: \(\left\{{}\begin{matrix}0,25x-1=0\\3-2y=0\end{matrix}\right.\Rightarrow\left\{{}\begin{matrix}0,25x=1\\2y=3\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}x=4\\y=\dfrac{3}{2}\end{matrix}\right.\)

Vậy: \(x=4;y=\dfrac{3}{2}\).

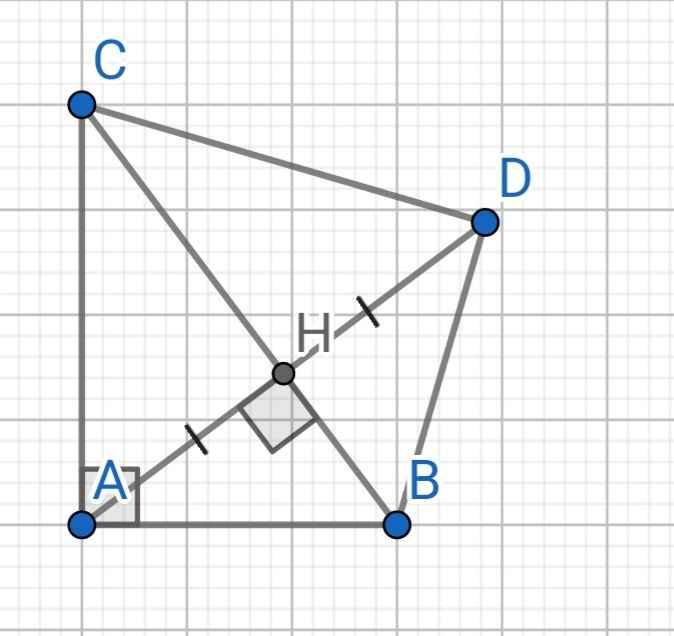 a) Xét hai tam giác vuông: ∆ABH và ∆DBH có:

BH là cạnh chung

HA = HD (gt)

⇒ ∆ABH = ∆DBH (hai cạnh góc vuông)

⇒ ∠ABH = ∠DBH (hai góc tương ứng)

⇒ BH là tia phân giác của ∠ABD

b) Do ∆ABH = ∆DBH (cmt)

⇒ AB = DB (hai cạnh tương ứng)

Do ∠ABH = ∠DBH (cmt)

⇒ ∠ABC = ∠DBC

Xét ∆ABC và ∆DBC có:

AB = DB (cmt)

∠ABC = ∠DBC (cmt)

AC là cạnh chung

⇒ ∆ABC = ∆DBC (c-g-c)

c) Do ∆ABC = ∆DBC (cmt)

⇒ ∠BAC = ∠BDC = 90⁰ (hai góc tương ứng)

⇒ BD ⊥ CD

Lời giải:
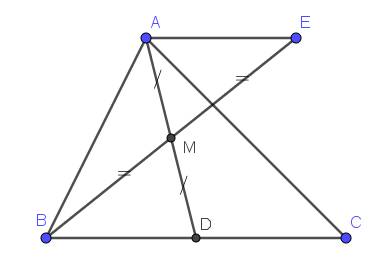
Xét tam giác $BMD$ và $EMA$ có:

$\widehat{BMD}=\widehat{EMA}$ (đối đỉnh) 

$BM=EM$ (gt) 

$MD=MA$ (do $M$ là trung điểm $AD$)

$\Rightarrow \triangle BMD=\triangle EMA$ (c.g.c)

$\Rightarrow BD=EA$ (đpcm)

và $\widehat{MBD}=\widehat{MEA}$

Mà 2 góc này ở vị trí so le trong nên $AE\parallel BD$ (đpcm)

Hình vẽ:

lên google mà tim câu trả lời

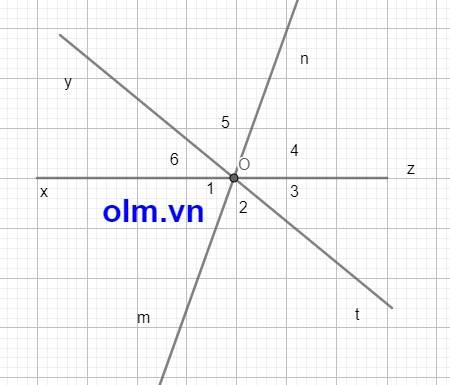
Vì góc yOz và góc xOy là hai góc kề bù nên Oz và Ox cùng nằm trên một đường thẳng zx (1) 

Tương tự ta có: Ot và Oy cùng nằm trên một đường thẳng

\(\widehat{xOt}\) và \(\widehat{yOz}\) là hai góc đối đỉnh

⇒ \(\widehat{O_2}\) = \(\dfrac{1}{2}\) \(\widehat{xOt}\) = \(\dfrac{1}{2}\) \(\widehat{yOz}\) = \(\widehat{O_5}\)

Mặt khác ta có: \(\widehat{O_2}\) + \(\widehat{O_1}\) + \(\widehat{O_6}\) = 180⁰ (gt)

                     ⇒ \(\widehat{O_1}\) + \(\widehat{O_6}\) + \(\widehat{O_5}\) ₌ 180⁰ 

                    ⇒ Om và On cùng thuộc một đường thẳng mn (2)

Kết hợp (1) và (2) ta có:   góc zOn và góc xOm là hai góc đối đỉnh

Để ngâm 1 kg mơ thì cần:

$4:3=\dfrac43$ (kg đường)

Để ngâm 2 kg mơ thì cần:

$\dfrac43\cdot2=\dfrac83$ (kg đường)

Vậy: ...

Nếu ngâm `1kg` mơ thì cần số đường là:

`4 : 3 = 4/3 (kg)`

Ngâm `2kg` mơ thì cần số đường là:

`4/3 . 2 = 8/6 (kg)`