Tử số chung là \(2^3.3^2.11=792\)

\(\dfrac{11}{13}=\dfrac{11x72}{13x72}=\dfrac{792}{936}\)

\(\dfrac{6}{8}=\dfrac{6x12x11}{8x12x11}=\dfrac{792}{1056}\)

\(\dfrac{4}{5}=\dfrac{4x18x11}{5x18x11}=\dfrac{792}{990}\)

\(\dfrac{8}{9}=\dfrac{8x9x11}{9x9x11}=\dfrac{792}{891}\)

\(\dfrac{9}{11}=\dfrac{9x8x11}{11x8x11}=\dfrac{792}{968}\)

11 = 1 \(\times\) 11; 6 = 2 \(\times\) 3; 8 = 2 \(\times\) 2  \(\times\) 2; 9 = 3 \(\times\) 3

Vậy tử số chung là: 11 \(\times\) 2 \(\times\)2 \(\times\) 2 \(\times\) 3 \(\times\) 3 = 792

\(\dfrac{11}{13}\) = \(\dfrac{11\times72}{13\times72}\) = \(\dfrac{792}{936}\)

\(\dfrac{6}{8}\) = \(\dfrac{6\times132}{8\times132}\) = \(\dfrac{792}{1056}\)

\(\dfrac{4}{5}\) = \(\dfrac{4\times198}{5\times198}\) = \(\dfrac{792}{990}\)

\(\dfrac{8}{9}\) = \(\dfrac{8\times99}{9\times99}\) = \(\dfrac{792}{891}\)

\(\dfrac{9}{11}\) = \(\dfrac{9\times88}{11\times88}\) = \(\dfrac{792}{968}\)

Gọi \(\widehat{aOc}\) là m, \(\widehat{cOb}\) là n

Ta có: \(m-n=90^o\)

mà \(m=180^o-n\) (2 góc bù nhau)

\(\Rightarrow180^o-n-n=90^o\\ \Leftrightarrow n=45^o\\ \Rightarrow m=90^o+45^o=135^o\)

Vậy \(\widehat{aOc}=135^o,\widehat{cOb}=45^o\)

Chiều dài HCN là :

\(6+4=10\left(cm\right)\)

Diện tích toàn phần :

\(126+2.6.10=246\left(m^2\right)\)

   \(\dfrac{1}{5\times6}+\dfrac{1}{6\times7}+\dfrac{1}{7\times8}+\dfrac{1}{8\times9}+\dfrac{1}{9\times10}\)

= \(\dfrac{1}{5}-\dfrac{1}{6}\times\dfrac{1}{6}-\dfrac{1}{7}\times\dfrac{1}{7}-\dfrac{1}{8}\times\dfrac{1}{8}-\dfrac{1}{9}\times\dfrac{1}{9}-\dfrac{1}{10}\)

= \(\dfrac{1}{5}-\dfrac{1}{10}\)  

= \(\dfrac{1}{10}\)

Bài tập cuối tuần 10

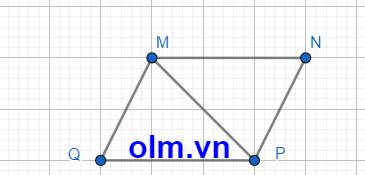
Xét \(\Delta\)MPQ và \(\Delta\)PMN có: 

MP chung

\(\widehat{QPM}\) = \(\widehat{PMN}\)  (2 góc so le trong)

\(\widehat{QMP}\) = \(\widehat{NPM}\) (2 góc so le trong)

\(\Rightarrow\) \(\Delta\)MPQ = \(\Delta\)PMN (g-c-g)

\(\Rightarrow\) PQ = MN; MQ = PN (đpcm)

b, Xét \(\Delta\)MPQ và \(\Delta\)PMN có:

         MP chung

         MN = PQ 

  \(\widehat{QPM}\) = \(\widehat{PMN}\) ( 2 góc so le trong)

⇒\(\Delta\)MPQ = \(\Delta\)PMN ( cạnh góc cạnh)

\(\Rightarrow\) MQ = NP (đpcm)

⇒ \(\widehat{QMP}\) = \(\widehat{NPM}\) 

   Mà hai góc \(\widehat{QMP}\) và \(\widehat{NPM}\) ở vị trí so le trong và bằng nhau nên:

   QM // NP (đpcm)

mik lm nếu bn like =)

Bài 4:
a) Ta có tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc CAE + góc BAC = 90 độ, tức là EC vuông góc với BC.

b) Vì tam giác ABC vuông cân tại A, nên góc BAC = 45 độ. Vì tam giác ACE vuông cân tại E, nên góc CAE = 45 độ. Từ đó suy ra góc BAE = góc BAC + góc CAE = 45 độ + 45 độ = 90 độ. Do đó, tứ giác ABCE là tứ giác vuông.

Bài 5:
a) Gọi K là giao điểm của đường thẳng AM và BH. Ta cần chứng minh góc BAK = góc CAK.
Vì CM = CA, ta có góc CMA = góc CAM. Vì đường thẳng AM song song với CA, nên góc CMA = góc KAB (do AB cắt đường thẳng AM tại I). Từ đó suy ra góc CAM = góc KAB.
Vì AH là đường cao, nên góc BAH = góc CAH. Từ đó suy ra góc BAK = góc CAK.
Vậy, AM là phân giác của góc BAH.

b) Ta có AB + AC = AB + AH + HC = BH + HC > BC (theo bất đẳng thức tam giác).
Vậy, luôn luôn có AB + AC < AH + BC.

a) Số gà mái là:

\(35+105=140\left(con\right)\)

Tỉ số phần trăm giữa gà trống và gà mái là:

\(\dfrac{35\times100}{140}=25\%\)

b) Tổng số gà của đàn gà:

\(140+35=175\left(con\right)\)

Số gà mái chiếm số phần trăm là:

\(\dfrac{140\times100}{175}=80\%\)

a, Số gà mái là:

35 + 105 = 140 ( con )

Tỉ số phần trăm của số gà trống và số gà mái là:

           35 : 140 x 100 = 25 %

b, Cả đàn gà có số con gà là:

           140 + 35 = 175 ( con gà )

   Số gà mái chiếm sô phần trăm số gà của cả đàn gà là:

           140 : 175 x 100 = 80%

                                   Đáp số: a, 25%

                                             b, 80%

Số lít nước mắm loại hai là:

\(10-4=6\left(l\right)\)

Tỉ số phần trăm giữa nước mắm loại một và nước mắm loại hai là:

\(\left(4\times100\%\right):6=66,7\%\)

Mẹ mua số l nc mắm loại 2 là :

   10 - 4 = 6 ( l )

Tỉ số phần trăm giữa nc mắm loại 1 và loại 2 là :

   4 : 6 = 66,66.

    Đ/S:..

Ta có:

\(\dfrac{13}{18}=\dfrac{13\times21}{18\times21}=\dfrac{273}{378}\)

\(\dfrac{13}{17}=\dfrac{13\times21}{17\times21}=\dfrac{273}{357}\)

\(\dfrac{21}{x}=\dfrac{21\times13}{x\times13}=\dfrac{273}{13x}\)

Ta được:

\(357<13x<378\)

\(357:13<x<378:13\)

\(27,46<x<29\) (làm tròn)

Mà \(27,46<28<29\)

Vậy số thích hợp là \(28\)