Tìm min
F=3x^2 +x -2
G= 4x^2+2x-1
H=5x^2-x+1
Tìm max
A= -x^2 -6x+3
B=-x^2+8x-1
C= -x^2-3X+4
D= -2x^2+3x-1
E= -3x^2 – x +2
F= -5x^2 -4x +3
G= -3x^2 – 5x+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo nha, tuy ko trùng đề lắm
Gọi trung điểm dường cheo AC, BD lần lượt là M, N
MN cắt AB, CD lần lượt ở I, K
Ta cần chứng minh góc NIB = góc MKC
Lấy H là trung điểm BC. Nối MH, NH.
Xét tam giac ABC có AM = MC ; CH = HB => MH là đường trung bình tam giác ABC => MH =AB/2 (1) và MH // AB => góc KMH = góc INH (2)
chung minh tuong tu ta có: NH = CD/2 (3)và NH // CD =>góc INH = góc MKC (4)
Mat khac từ (1)và (3) ta có NH = MH vì đều bằng một nửa AB và CD => tam giác MHN cân tại H => góc NMH = góc MNH =>góc KMH = góc INH (vì kể với 2 góc bằng nhau) (5)
Từ (3)(4)(5) => góc MKC = góc NIB (đpcm)

Vì \(P\left(x\right)⋮\left(2x-1\right)\) \(\Rightarrow P\left(\dfrac{1}{2}\right)=0\)
Xét đa thức \(Q\left(x\right)=P\left(x\right)-\left(x+1\right)\). Ta có \(Q\left(1\right)=Q\left(2\right)=Q\left(3\right)=Q\left(4\right)=0\) nên \(Q\left(x\right)\) có 4 nghiệm là \(1,2,3,4\). Nếu \(Q\left(x\right)\equiv0\) thì \(P\left(x\right)=x+1\), vô lý. Do đó \(Q\left(x\right)\) là đa thức khác hằng \(\Rightarrow\) bậc của \(Q\left(x\right)\) phải lớn hơn hoặc bằng 4. Mà \(P\left(x\right)\) có hệ số cao nhất là 1 \(\Rightarrow\) \(Q\left(x\right)\) cũng phải có hệ số cao nhất là 1.
Mặt khác, \(Q\left(\dfrac{1}{2}\right)=P\left(\dfrac{1}{2}\right)-\left(\dfrac{1}{2}+1\right)=-\dfrac{3}{2}\)
Đặt \(Q\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)R\left(x\right)\). Khi đó \(R\left(x\right)\) có hệ số cao nhất là 1 và \(R\left(\dfrac{1}{2}\right)=-\dfrac{8}{35}\).
Khi đó, ycbt \(\Leftrightarrow\) tìm tất cả các đa thức \(R\left(x\right)\) có hệ số cao nhất là 1 mà \(R\left(\dfrac{1}{2}\right)=-\dfrac{8}{35}\).
Nếu \(R\left(x\right)=-\dfrac{8}{35}\) thì vô lý.
Nếu \(R\left(x\right)\) có bậc là 1 thì \(R\left(x\right)=x+a\). Thế \(x=\dfrac{1}{2}\) sẽ tìm được \(a=-\dfrac{51}{70}\) và do đó \(R\left(x\right)=x-\dfrac{51}{70}\) \(\Rightarrow Q\left(x\right)=\left(x-1\right)\left(x-2\right)\left(x-3\right)\left(x-4\right)\left(x-\dfrac{51}{70}\right)\). Thế vào \(Q\left(x\right)=P\left(x\right)-\left(x+1\right)\) ta tìm được đa thức \(P\left(x\right)\) thỏa ycbt.
Nếu \(R\left(x\right)\) có bậc 2 thì \(R\left(x\right)=x^2+ax+b\). Thế \(x=\dfrac{1}{2}\) thì ta có \(\dfrac{1}{2}a+b=-\dfrac{1}{2}\), sẽ có vô số cặp số \(\left(a,b\right)\) thỏa mãn điều này \(\Rightarrow\) tồn tại vô số đa thức \(Q\left(x\right)\) \(\Rightarrow\) tồn tại vô số đa thức \(P\left(x\right)\) thỏa ycbt.
Tương tự như thế, ta xét bậc của \(R\left(x\right)\) tăng dần thì sẽ có vô số đa thức \(P\left(x\right)\) thỏa mãn ycbt. (nhưng sẽ không có công thức chung cho các đa thức)
Vì �(�)⋮(2�−1)P(x)⋮(2x−1) ⇒�(12)=0⇒P(21)=0
Xét đa thức �(�)=�(�)−(�+1)Q(x)=P(x)−(x+1). Ta có �(1)=�(2)=�(3)=�(4)=0Q(1)=Q(2)=Q(3)=Q(4)=0 nên �(�)Q(x) có 4 nghiệm là 1,2,3,41,2,3,4. Nếu �(�)≡0Q(x)≡0 thì �(�)=�+1P(x)=x+1, vô lý. Do đó �(�)Q(x) là đa thức khác hằng ⇒⇒ bậc của �(�)Q(x) phải lớn hơn hoặc bằng 4. Mà �(�)P(x) có hệ số cao nhất là 1 ⇒⇒ �(�)Q(x) cũng phải có hệ số cao nhất là 1.
Mặt khác, �(12)=�(12)−(12+1)=−32Q(21)=P(21)−(21+1)=−23
Đặt �(�)=(�−1)(�−2)(�−3)(�−4)�(�)Q(x)=(x−1)(x−2)(x−3)(x−4)R(x). Khi đó �(�)R(x) có hệ số cao nhất là 1 và �(12)=−835R(21)=−358.
Khi đó, ycbt ⇔⇔ tìm tất cả các đa thức �(�)R(x) có hệ số cao nhất là 1 mà �(12)=−835R(21)=−358.
Nếu �(�)=−835R(x)=−358 thì vô lý.
Nếu �(�)R(x) có bậc là 1 thì �(�)=�+�R(x)=x+a. Thế �=12x=21 sẽ tìm được �=−5170a=−7051 và do đó �(�)=�−5170R(x)=x−7051 ⇒�(�)=(�−1)(�−2)(�−3)(�−4)(�−5170)⇒Q(x)=(x−1)(x−2)(x−3)(x−4)(x−7051). Thế vào �(�)=�(�)−(�+1)Q(x)=P(x)−(x+1) ta tìm được đa thức �(�)P(x) thỏa ycbt.
Nếu �(�)R(x) có bậc 2 thì �(�)=�2+��+�R(x)=x2+ax+b. Thế �=12x=21 thì ta có 12�+�=−1221a+b=−21, sẽ có vô số cặp số (�,�)(a,b) thỏa mãn điều này ⇒⇒ tồn tại vô số đa thức �(�)Q(x) ⇒⇒ tồn tại vô số đa thức �(�)P(x) thỏa ycbt.
Tương tự như thế, ta xét bậc của �(�)R(x) tăng dần thì sẽ có vô số đa thức �(�)P(x) thỏa mãn ycbt. (nhưng sẽ không có công thức chung cho các đa thức)

Ta thấy
\(f\left(x\right):g\left(x\right)\)
\(\Rightarrow\left(x^{100}+x^{99}+x^{98}+x^5+2020\right):\left(x^2-1\right)\)
\(=\left(x^{98}+x^{97}+2x^{96}+2x^{95}+...2x^4+3x^3+2x^2+3x+2\right)\) có số dư là \(R\left(x\right)=3x+2022\)
\(\Rightarrow R\left(2021\right)=3.2021+2022=8085\)


Bài 1:
a, \(x^3\) + y3 + \(x\) + y
= (\(x^3\) + y3) + (\(x\) + y)
= (\(x\) + y)(\(x^2\) - \(xy\) + y2) + (\(x\) + y)
= (\(x\) + y)( \(x^2-xy+y^2\)+1)
b, \(x^3\) + 4\(x^2\)y + 4\(xy^2\) - 9\(x\)
= \(x\)(\(x^2\) + 4\(xy\) + 4y2 - 9)
= \(x\)[ (\(x\) + 2y)2 - 32)
= \(x\)[ (\(x\) + 2y - 3).( \(x\) + 2y + 3)]

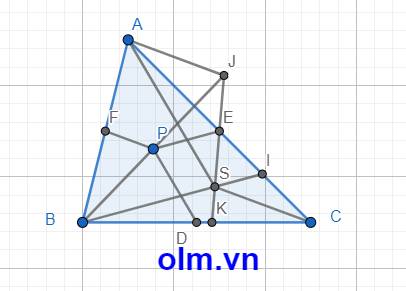
Gọi J là giao điểm của BP và KE; Xét \(\Delta\)BSJ có:
PE // BS; PE = \(\dfrac{1}{2}\) BS
⇒ PF là đường trung bình của \(\Delta\)BSJ (vì đường trung bình của tam giác thì song song với cạnh thứ ba và bằng nửa cạnh ấy)
⇒ PJ = PB; EJ = ES (1)
Xét \(\Delta\)ABJ có: AF = FB (gt); PJ = PB theo (1)
⇒ PF là đường trung bình của \(\Delta\) ABJ (vì đường trung bình của tam giác đi qua trung điểm hai cạnh của tam giác và song song với cạnh còn lại)
⇒ PF// AJ (2)
Xét tứ giác ASCJ ta có: E là giao điểm hai đường chéo
AE = EC (gt)
EJ = ES ( theo (1)
⇒ Tứ giác ASCJ là hình bình hành vì tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường thì tứ giác đó là hình bình hành.
⇒ CS // CJ (3)
Kết hợp (2) và(3) ta có:
CS // PF ( vì trong cùng một mặt phẳng hai đường thẳng cùng song song với đường thẳng thứ ba thì song song với nhau.)
Kết luận: nếu BS = 2EP thì CS // PF điều phải chứng minh
Tìm min:
$F=3x^2+x-2=3(x^2+\frac{x}{3})-2$
$=3[x^2+\frac{x}{3}+(\frac{1}{6})^2]-\frac{25}{12}$
$=3(x+\frac{1}{6})^2-\frac{25}{12}\geq \frac{-25}{12}$
Vậy $F_{\min}=\frac{-25}{12}$. Giá trị này đạt tại $x+\frac{1}{6}=0$
$\Leftrightarrow x=\frac{-1}{6}$
Tìm min
$G=4x^2+2x-1=(2x)^2+2.2x.\frac{1}{2}+(\frac{1}{2})^2-\frac{5}{4}$
$=(2x+\frac{1}{2})^2-\frac{5}{4}\geq 0-\frac{5}{4}=\frac{-5}{4}$ (do $(2x+\frac{1}{2})^2\geq 0$ với mọi $x$)
Vậy $G_{\min}=\frac{-5}{4}$. Giá trị này đạt tại $2x+\frac{1}{2}=0$
$\Leftrightarrow x=\frac{-1}{4}$