Những số nào thuộc tập hợp ƯC(36,12)(36,12)?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Giải:
a, Nam đã gấp số con hạc là: 35 - 5 = 30 (con )
b , Để gấp đủ 45 con Hạc Nam cần thêm số tờ giấy màu là:
45 - 35 = 10 (tờ)
Đs...

1. phép cộng của 3 số khác nhau có tổng bằng 6 là:
1+2+3
2. phép cộng của 4 số khác nhau có tổng bằng 6 là:
0+1+2+3

Số tự nhiên n thỏa mãn \(n^k\left(k\inℕ^∗\right)\) có tận cùng là 9 khi và chỉ khi \(n\) có chữ số tận cùng là 3, 7 hoặc 9.
TH1: Nếu \(n\) có chữ số tận cùng là \(3\) thì ta có nhận xét là \(n^{4k}\) có chữ số tận cùng là 1 với mọi số tự nhiên \(k\). Thật vậy, với \(k=0\) thì \(n^0=1\) có tận cùng là 9. Giả sử khẳng định đúng đến \(k=l\). Với \(k=l+1\) thì \(n^{4\left(l+1\right)}=n^{4l+4}=n^4.n^{4l}=\overline{A1}.\overline{B1}\) có chữ số tận cùng là 1. Vậy khẳng định được chứng minh. Do đó, \(n^{9012}=n^{4.2253}\) có chữ số tận cùng là 1, không thỏa ycbt.
TH2: \(n\) có chữ số tận cùng là 7 thì làm tương tự với TH1, \(n^{4k}\) luôn có chữ số tận cùng là 7 nên không thỏa ycbt.
TH3: \(n\) có chữ số tận cùng là 9 thì \(n^{2k}\) luôn có chữ số tận cùng là 1. Như vậy, không thể có số tự nhiên \(n\) nào thỏa mãn ycbt.

Để olm giúp em nhá
(9989)69 = 996141 = (992)3070.99 = (\(\overline{..01}\))3070.99 = \(\overline{..99}\)
62021 = (65)404.6 = 7776404.6 = \(\overline{...76}.6\) = \(\overline{...56}\)
A=142022.162022=(14.16)2022=2242022= (2242)1001= \(\overline{...76}\)1001=\(\overline{...76}\)

Đổi 10cm= 1dm
Cạnh đáy bể:
20:4=5(dm)
Diện tích đáy bể:
5 x 5 = 25(dm2)
Thể tích viên đá:
25 x 1= 25(dm3)
Đ.số:25 dm3

Theo đề \(A\) có \(N\) chữ số, \(A^5\) có \(M\) chữ số
Nên \(\left[{}\begin{matrix}M=N\\M=N+1\end{matrix}\right.\) (chữ số)
\(\Rightarrow\left[{}\begin{matrix}M+2N=N+2N=3N=169\\M+2N=N+2\left(N+1\right)=3N+2=169\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}N=169:3\left(loại\right)\\N=167:3\left(loại\right)\end{matrix}\right.\) (Vì \(N\inℕ\))
Vậy không tồn tại \(M+2N=169\) như theo đề bài.

\(\left(a-1\right)^2\ge0\Rightarrow a^2+1-2a\ge0\Rightarrow a^2+1\ge2a\left(1\right)\)
\(\left(2b-3\right)^2\ge0\Rightarrow4b^2+9-12b\ge0\Rightarrow4b^2+9\ge12b\left(2\right)\)
\(\left(c\sqrt[]{3}-\sqrt[]{3}\right)^2\ge0\Rightarrow3c^2+3-6c\ge0\Rightarrow3c^2+3\ge6c\left(3\right)\)
\(\left(1\right)+\left(2\right)+\left(3\right)\Rightarrow a^2+1+4b^2+9+3c^2+3\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2+1+9+3\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2+13\ge2a+12b+6c\)
\(\Rightarrow a^2+4b^2+3c^2\ge2a+12b+6c-13\)
mà \(2a+12b+6c-13>2a+12b+6c-14\)
\(\Rightarrow a^2+4b^2+3c^2>2a+12b+6c-14\)
\(\Rightarrow dpcm\)
⇔(a−1)2+(2b−3)2+3(c−1)2+1>0 (luôn đúng)
⇒⇒ BĐT ban đầu đúng

A = \(\dfrac{1}{2\times3}\) + \(\dfrac{1}{2\times4}\) + \(\dfrac{1}{3\times4}\)
A = \(\dfrac{1}{6}\) + \(\dfrac{1}{8}\) + \(\dfrac{1}{12}\)
A = \(\dfrac{4}{24}\) + \(\dfrac{3}{24}\) + \(\dfrac{2}{24}\)
A = \(\dfrac{9}{24}\)
A = \(\dfrac{3}{8}\)
Kết quả của phép tính sau khi rút gọn có mẫu số là 8
Đáp số: 8
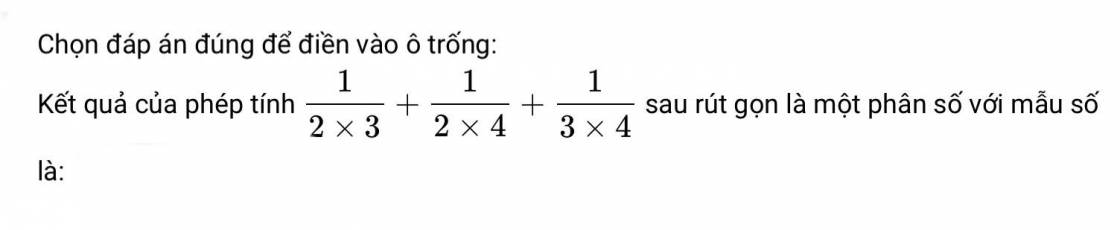
Tập hợp ƯC(36,12) là \(A=\left\{\pm1;\pm2;\pm3;\pm4;\pm6;\pm12\right\}\)