Trên quãng đường AC dài 200 km có một địa điểm B các A là 10 km. Lúc 7 giờ, một ô tô đi từ A, một ô tô khác đi từ B, cả hai cùng đi tới C với vận tốc thứ tự bằng 50 km/h và 40 km/h. Hỏi lúc mấy giờ thì khoảng cách đến C của xe thứ hai gấp đôi khoảng cách đến C của xe thứ nhất
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: \(\widehat{MON}+\widehat{O_1}+45^0=180^0\)
=>\(\widehat{O_1}=180^0-90^0-45^0=45^0\)
Ta có: \(\widehat{O_1}=\widehat{MNO}\left(=45^0\right)\)
mà hai góc này là hai góc ở vị trí so le trong
nên OB//AM
b: Ta có: OB//AM
MA\(\perp\)AB
Do đó: OB\(\perp\)BA

a: m\(\perp\)a
n\(\perp\)a
Do đó: m//n
b: m//n
=>\(\widehat{A_1}=\widehat{ABC}\)(hai góc so le trong)
=>\(\widehat{A_1}=72^0\)
c: Xét ΔABC có \(\widehat{BAC}+\widehat{ACB}+\widehat{ABC}=180^0\)
=>\(\widehat{C_1}=180^0-64^0-72^0=44^0\)

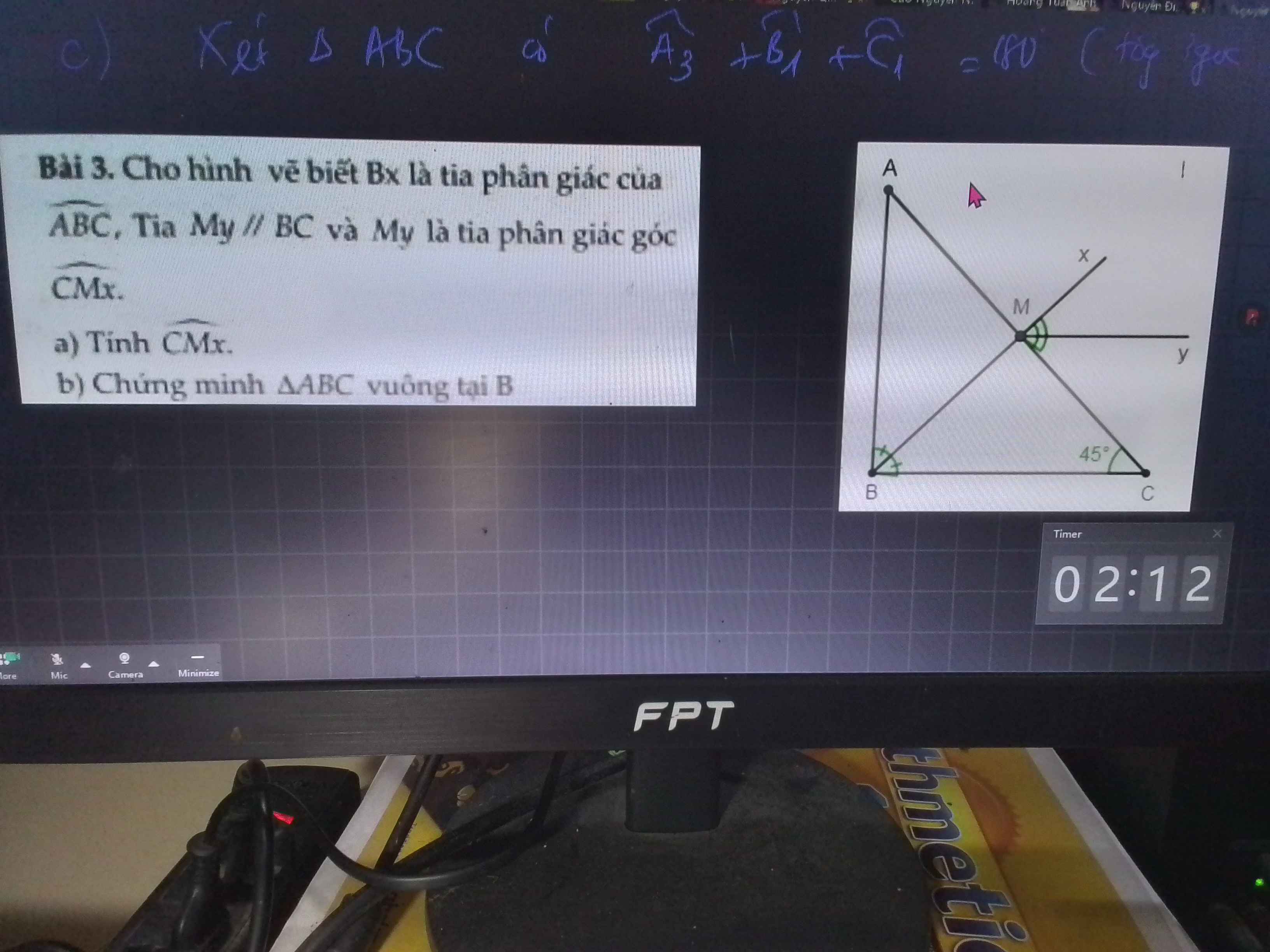
a.
Do \(My||BC\Rightarrow\widehat{CMy}=\widehat{MCB}\) (so le trong)
Mà \(\widehat{MCB}=45^0\Rightarrow\widehat{CMy}=45^0\)
lại có My là phân giác của \(\widehat{CMx}\Rightarrow\widehat{CMx}=2\widehat{CMy}\)
\(\Rightarrow\widehat{CMx}=2.45^0=90^0\)
b.
Do \(BC||My\Rightarrow\widehat{CBM}=\widehat{xMy}\)
Mà \(\widehat{xMy}=\widehat{CMy}=45^0\) (My là phân giác)
\(\Rightarrow\widehat{CBM}=45^0\)
Lại có Bx là phân giác \(\widehat{ABC}\Rightarrow\widehat{ABC}=2\widehat{CBM}\)
\(\Rightarrow\widehat{ABC}=2.45^0=90^0\)
\(\Rightarrow\Delta ABC\) vuông tại B

\(1,\dfrac{2}{3}+\dfrac{1}{3}:x=\dfrac{4}{3}\\ =>\dfrac{1}{3}:x=\dfrac{4}{3}-\dfrac{2}{3}\\ =>\dfrac{1}{3}:x=\dfrac{2}{3}\\ =>x=\dfrac{1}{3}:\dfrac{2}{3}=\dfrac{1}{2}\\ 2,\dfrac{4}{5}+\dfrac{1}{3}:x=\dfrac{2}{3}\\ =>\dfrac{1}{3}:x=\dfrac{2}{3}-\dfrac{4}{5}=-\dfrac{2}{15}\\ =>x=\dfrac{1}{3}:\dfrac{-2}{15}=\dfrac{-5}{2}\\ 3,\dfrac{2}{3}+\dfrac{5}{2}:x=\dfrac{3}{4}\\ =>\dfrac{5}{2}:x=\dfrac{3}{4}-\dfrac{2}{3}\\ =>\dfrac{5}{2}:x=\dfrac{1}{12}\\ =>x=\dfrac{5}{2}:\dfrac{1}{12}=30\)

\(\left(-5\right)^5=\left(-5\right)^4\cdot\left(-5\right)=5^4\cdot\left(-5\right)=625\cdot\left(-5\right)=-3125\)

a: \(x=\left(x^3\right)^{\dfrac{1}{3}}\)
b: \(x=\left(x^5\right)^{\dfrac{1}{5}}\)

\(\dfrac{1}{3^6}=\dfrac{1}{3^4\cdot3^2}=\dfrac{1}{81\cdot9}=\dfrac{1}{729}\)
\(\dfrac{1}{3^6}\) = \(\dfrac{1}{3^4.3^2}\) = \(\dfrac{1}{81.9}\) = \(\dfrac{1}{729}\)

a: \(\dfrac{\left(-1\right)^2}{2^2}=\dfrac{1}{4};\left(-\dfrac{1}{2}\right)^2=\dfrac{1}{4}\)
Do đó: \(\dfrac{\left(-1\right)^2}{2^2}=\left(-\dfrac{1}{2}\right)^2\)
b: \(\dfrac{3^3}{5^3}=\left(\dfrac{3}{5}\right)^3< \dfrac{3}{5}\)(do \(0< \dfrac{3}{5}< 1\))
d: \(\left(\dfrac{3}{4}\right)^7:\left(\dfrac{3}{4}\right)^3=\left(\dfrac{3}{4}\right)^4\)
Vì \(0< \dfrac{3}{4}< 1\)
nên \(\left(\dfrac{3}{4}\right)^4< \left(\dfrac{3}{4}\right)^2\)
=>\(\left(\dfrac{3}{4}\right)^7:\left(\dfrac{3}{4}\right)^3< \left(\dfrac{3}{4}\right)^2\)
e: \(\left(0,5\right)^6:\left(0,5\right)^2=\left(0,5\right)^{6-2}=\left(0,5\right)^4=\left(0,5\right)^{2\cdot2}=\left[\left(0,5\right)^2\right]^2\)

a: Ta có: \(\widehat{xOz}+\widehat{yOz}=180^0\)(hai góc kề bù)
=>\(\widehat{yOz}+50^0=180^0\)
=>\(\widehat{yOz}=130^0\)
b: Sửa đề: \(\widehat{OKt}=130^0\)
Ta có: \(\widehat{tKO}+\widehat{xOK}=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên Kt//Ox