Trên cùng một nửa mặt phẳng bờ chứa tia Ox vẽ hai tia Ot Oy sao cho xOt=50 độ xOy= 120 độ
a) trong ba tia Ox,Oy,Ot thì tia nào nằm giữa 2 tia còn lại?Vì sap?
b)Tính số đo góc yOt
c)Vẽ tia Oz là tia đối của tia Ox.Tính số đo của góc tOz?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giải:
Thời gian người đó đi hết quãng đường AB không kể thời gian nghỉ là:
10 giờ 15 phút - 6 giờ 30 phút - 15 phút = 3 giờ 30 phút
Đổi 3 giờ 30 phút = 3,5 giờ
Quãng đường AB dài là:
42 x 3,5 = 147 (km)
Đáp số: 147 km
Thời gian người đó đi hết quãng đường AB không kể thời gian nghỉ là:
10 giờ 15 phút - 6 giờ 30 phút - 15 phút = 3 giờ 30 phút
Đổi 3 giờ 30 phút = 3,5 giờ
Quãng đường AB dài là:
42 x 3,5 = 147 (km)
Đáp số: 147 km
k ạ. Mik lm hơi muộn

ột hình hộp chữ nhật có chiều dài 36cm, chiều dài gấp đôi chiều rộng và gấp 4 lần chiều cao. Tính diện tích xung quanh của hình hộp đó.
giúp mik nha

m3 = 75.n (m; n ϵ N*)
m3 - 75n = 0
Ta có: 75 = 1 x 75 = 3 x 25 = 15 x 5
Lập phương nhỏ nhất từ các tích trên:
\(1\times75\rightarrow75^3\)
\(3\times25\rightarrow75^3\)
\(15\times5\rightarrow15\times5\times3\times15\rightarrow15^3\)
Do 153 là giá trị nhỏ nhất ⇒ m = 15
⇒ n = 153 : 75 = 45
Vậy m = 15 và n = 45.

\(x\times\left(\dfrac{1}{3}+\dfrac{1}{15}+\dfrac{1}{35}+\dfrac{1}{49}+\dfrac{1}{63}+\dfrac{1}{99}\right)=920\)
\(x\times\left(\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+\dfrac{1}{7\times9}+\dfrac{1}{9\times11}\right)=920\\ x\times\left(1-\dfrac{1}{11}\right)=920\\ x\times\dfrac{10}{11}=920\\ x=1012.\)

\(2\left(x+\dfrac{-5}{2}\right)^2+\dfrac{-5}{12}=\dfrac{1}{12}\)
=>\(2\left(x-\dfrac{5}{2}\right)^2=\dfrac{1}{12}+\dfrac{5}{12}=\dfrac{6}{12}=\dfrac{1}{2}\)
=>\(\left(x-\dfrac{5}{2}\right)^2=\dfrac{1}{4}\)
=>\(\left[{}\begin{matrix}x-\dfrac{5}{2}=\dfrac{1}{2}\\x-\dfrac{5}{2}=-\dfrac{1}{2}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=2\end{matrix}\right.\)

4550 - 4 x 155 - 6 x 155 = ?
4550 - (4 + 6) x 155 = ?
4550 - 10 x 155 = ?
4550 - 1550 = 3000
4550 - 4 x 155 - 6 x 155 = ?
4550 - (4 + 6) x 155 = ?
4550 - 10 x 155 = ?
4550 - 1550 = 3000

\(A=\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< 1\)
Đặt \(S=\dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)
Ta có:
\(S=1-\dfrac{1}{2}+\dfrac{1}{2}-\dfrac{1}{3}+...+\dfrac{1}{99}-\dfrac{1}{100}\)
\(S=1-\dfrac{1}{100}\)
\(S=\dfrac{99}{100}\)
mà
\(\dfrac{1}{2^2}=\dfrac{1}{1.2}\)
\(\dfrac{1}{3^2}< \dfrac{1}{3.2}\)
\(\dfrac{1}{4^2}< \dfrac{1}{3.4}\)
...
\(\dfrac{1}{100^2}< \dfrac{1}{99.100}\)
\(\Rightarrow\dfrac{1}{2^2}+\dfrac{1}{3^2}+\dfrac{1}{4^2}+...+\dfrac{1}{100^2}< \dfrac{1}{1.2}+\dfrac{1}{2.3}+\dfrac{1}{3.4}+...+\dfrac{1}{99.100}\)
\(\Rightarrow A< S\)
\(=>A=\dfrac{99}{100}\)
\(=>A< 1\left(đpcm\right)\)

Câu 1:
\(\dfrac{6}{-15}\) = \(\dfrac{6:3}{-15:3}\) = \(\dfrac{2}{-5}\);
\(\dfrac{-4}{-12}\) = \(\dfrac{-4:-4}{12:-4}\) = \(\dfrac{1}{3}\) > \(\dfrac{2}{-5}\)
\(\dfrac{-14}{35}\) = \(\dfrac{-14:-7}{35:-7}\) = \(\dfrac{2}{-5}\)
- 0,4 = \(\dfrac{2}{-5}\)
\(\dfrac{17}{40}\)> \(\dfrac{16}{40}\) ⇒ \(\dfrac{-17}{40}\) < \(\dfrac{-16}{40}\) (Vì khi nhân cả hai vế bất đẳng thức với một số âm thì dấu của bất đẳng thức đổi chiều)
⇒ \(\dfrac{-17}{40}\) < \(\dfrac{-16}{40}\) = \(\dfrac{-16:\left(-8\right)}{40:\left(-8\right)}\) = \(\dfrac{2}{-5}\)
40% = \(\dfrac{40}{100}\) = \(\dfrac{2}{5}\) > \(\dfrac{2}{-5}\)
Từ những lập luận trên ta có trong các phân số đã cho phân số biểu diễn cho số hữu tỉ \(\dfrac{2}{-5}\) lần lượt là các phân số sau:
\(\dfrac{6}{-15}\); \(\dfrac{-14}{35}\); -0,4
Bài 2:
a; Sắp xếp các phân số sau theo thứ tự tăng dần:
3,25; 3\(\dfrac{4}{5}\); \(\dfrac{-5}{2}\); 140%; -2
\(\dfrac{5}{2}\) > \(\dfrac{4}{2}\) (hai phân số dương, hai phân số có cùng mẫu số phân số nào có tử số lớn hơn thì phân số đó lớn hơn.
⇒ \(\dfrac{5\times-1}{2}\) < \(\dfrac{4\times-1}{2}\) (vì khi nhân hai vế với cùng một số âm thì dấu của bất đẳng thức đổi chiều)
⇒ \(\dfrac{-5}{2}\) < \(\dfrac{-4}{2}\) = - 2 < 0 (phân số âm luôn nhỏ hơn 0)
3\(\dfrac{4}{5}\) = 3,8; 140% = 1,4 vì 3,8 > 3,25 > 1,4 > 0
⇒ \(3\dfrac{4}{5}\) > 3,25 > 140% > 0
Từ những lập luận trên ta có:
\(\dfrac{-5}{2}\) < -2 < 0 < 140% < 3,25 < 3\(\dfrac{4}{5}\)
Vậy các phân số đã cho được sắp xếp theo thứ tự tăn dần lần lượt là:
\(\dfrac{-5}{2}\); -2; 140%; 3,25; 3\(\dfrac{4}{5}\)
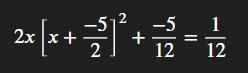


a: Trên cùng một nửa mặt phẳng bờ chứa tia Ox, ta có: \(\widehat{xOt}< \widehat{xOy}\left(50^0< 120^0\right)\)
nên tia Ot nằm giữa hai tia Ox và Oy
b: Ta có: tia Ot nằm giữa hai tia Ox và Oy
=>\(\widehat{xOt}+\widehat{tOy}=\widehat{xOy}\)
=>\(\widehat{tOy}+50^0=120^0\)
=>\(\widehat{tOy}=70^0\)
c: Ta có: \(\widehat{xOt}+\widehat{tOz}=\widehat{xOz}\)
=>\(\widehat{tOz}+50^0=180^0\)
=>\(\widehat{tOz}=130^0\)