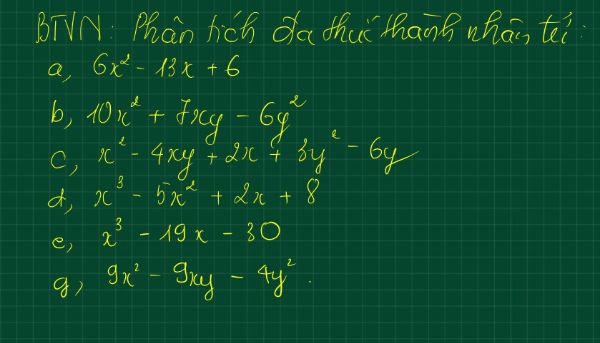cho a, b,c là độ dài ba cạnh của 1 tam giác, chứng minh rằng a mũ 3 + b mũ 3 + 3abc>c mũ 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
8 tháng 10 2021
Bài 1
Áp dụng hằng đẳng thức
\(x^3+x^2+x=x\left(x^2+2x+1\right)=x\left(x+1\right)^2\)
Bài 2
\(\left(87^2-27^2\right)+\left(73^2-13^2\right)=6840-5160=1680\)
8 tháng 10 2021
a.
−−→AM+−−→BN+−−→CP=12−−→AB+12−−→AC+12−−→BA+12−−→BC+12−−→CA+12−−→CBAM→+BN→+CP→=12AB→+12AC→+12BA→+12BC→+12CA→+12CB→
=12(−−→AB+−−→BA)+12(−−→BC+−−→CB)+12(−−→AC+−−→CA)=→0=12(AB→+BA→)+12(BC→+CB→)+12(AC→+CA→)=0→
b.
Ta có:
−−→GM+−−→GN+−−→GP=−−→GA+−−→AM+−−→GB+−−→BN+−−→GC+−−→CPGM→+GN→+GP→=GA→+AM→+GB→+BN→+GC→+CP→
=(−−→GA+−−→GB+−−→GC)+(−−→AM+−−→BN+−−→CP)=→0+→0=→0=(GA→+GB→+GC→)+(AM→+BN→+CP→)=0→+0→=0→
⇒G⇒G là trọng tâm tam giác MNP
CT
8 tháng 10 2021
Do M và N lần lượt là trung điểm của BC và AC nên MN là đường trung bình của tam giác AB.
đđây nhá !
8 tháng 10 2021
a)A=−x2−2x+5a)A=−x2−2x+5
=−x2−2x−1+6=−x2−2x−1+6
=−(x2+2x+1)+6=−(x2+2x+1)+6
=−(x+1)2+6=−(x+1)2+6
Ta có: (x+1)2(x+1)2 ≥0≥0
-> −(x+1)2−(x+1)2 ≤0≤0
-> −(x+1)2+6−(x+1)2+6 ≤6≤6
Dấu bằng xảy ra khi: x+1=0x+1=0
⇔ x=−1x=−1
b)B=9x−3x2+4b)B=9x−3x2+4
=−3x2+9x−=−3x2+9x− 274+274+ 434434
=−(3x2−9x+274)+434=−(3x2−9x+274)+434
=−3(x2−3x+94)+434=−3(x2−3x+94)+434
=−3(x−32)2+434=−3(x−32)2+434
Ta có: (x−32)2(x−32)2 ≥0≥0
-> −3(x−32)2−3(x−32)2 ≤0≤0
-> −3(x−32)2+434−3(x−32)2+434 ≤434≤434
Dấu bằng xảy ra khi: x−32=0x−32=0
⇔ x=32x=32
Chúc bạn học tốt !!!!!
giup toi lam bai nay coi
MH
1
DD
Đoàn Đức Hà
Giáo viên
8 tháng 10 2021
a) \(6x^2-13x+6=6x^2-4x-9x+6=2x\left(3x-2\right)-3\left(3x-2\right)=\left(2x-3\right)\left(3x-2\right)\)
b) \(10x^2-5xy+12xy-6y^2=5x\left(2x-y\right)+6y\left(2x-y\right)=\left(5x+6y\right)\left(2x-y\right)\)
c) \(x^2-4xy+2x+3y^2-6y=x^2-3xy-xy+3y^2+2x-6y\)
\(=x\left(x-3y\right)-y\left(x-3y\right)+2\left(x-3y\right)\)
\(=\left(x-y+2\right)\left(x-3y\right)\)
d) \(x^3-5x^2+2x+8=x^3+x^2-6x^2-6x+8x+8\)
\(=\left(x+1\right)\left(x^2-6x+8\right)=\left(x+1\right)\left(x^2-2x-4x+8\right)\)
\(=\left(x+1\right)\left(x-2\right)\left(x-4\right)\)
e) \(x^3-19x-30=x^3-5x^2+5x^2-25x+6x-30\)
\(=\left(x-5\right)\left(x^2+5x+6\right)=\left(x-5\right)\left(x^2+2x+3x+6\right)\)
\(=\left(x-5\right)\left(x+2\right)\left(x+3\right)\)
g) \(9x^2-9xy-4y^2=9x^2+3xy-12xy-4y^2\)
\(=\left(3x+y\right)\left(3x-4y\right)\)