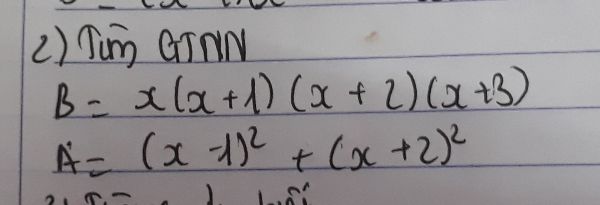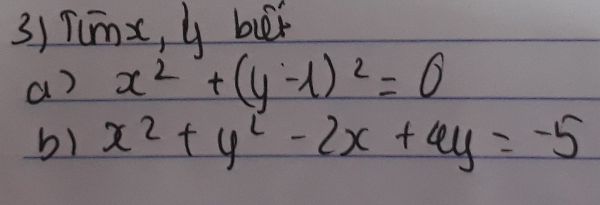Ta xét VT:

\(a^2\left(b-c\right)+b^2\left(c-a\right)+c^2\left(a-b\right)=a^2b-a^2c+b^2c-ab^2+ac^2-bc^2\)

Ta xét VP:

\(\left(a-b\right)\left(b-c\right)\left(a-c\right)=\left(ab-ac-b^2+bc\right)\left(a-c\right)\)

\(=a^2b-a^2c-ab^2+abc-abc+ac^2+b^2c-bc^2\)

\(=a^2b-a^2c+b^2c-ab^2+ac^2-bc^2\)

Ta thấy: VT = VP 

\(\Rightarrowđpcm\)

\(\left(x-1\right)\left(x^2+x+1\right)-x\left(x+2\right)\left(x-2\right)=5\)

\(\Rightarrow\left(x-1\right)\left(x^2+x1+1^3\right)-x\left(x^2-4\right)=5\)

\(\Rightarrow x^3-1-x^3+4x=5\)

\(\Rightarrow4x-1=5\)

\(\Rightarrow4x=6\)

\(\Rightarrow x=\frac{3}{2}\)

????????

là sao bn ơi ? mà câu hỏi đâu ?

3) 

a) \(x^2+\left(y-1\right)^2=0\)

\(\Leftrightarrow\hept{\begin{cases}x=0\\y-1=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x=0\\y=1\end{cases}}\).

b) \(x^2+y^2-2x+4y=-5\)

\(\Leftrightarrow x^2-2x+1+y^2+4y+4=0\)

\(\Leftrightarrow\left(x-1\right)^2+\left(y+2\right)^2=0\)

\(\Leftrightarrow\hept{\begin{cases}x-1=0\\y+2=0\end{cases}}\)

\(\Leftrightarrow\hept{\begin{cases}x=1\\y=-2\end{cases}}\).

2) 

\(B=x\left(x+1\right)\left(x+2\right)\left(x+3\right)=\left[x\left(x+3\right)\right]\left[\left(x+1\right)\left(x+2\right)\right]\)

\(=\left(x^2+3x\right)\left(x^2+3x+2\right)=\left(x^2+3x+1-1\right)\left(x^2+3x+1+1\right)\)

\(=\left(x^2+3x+1\right)^2-1\ge-1\)

Dấu \(=\)khi \(x^2+3x+1=0\Leftrightarrow x=\frac{-3\pm\sqrt{5}}{2}\).

\(A=\left(x-1\right)^2+\left(x+2\right)^2=\left(x+\frac{1}{2}-\frac{3}{2}\right)^2+\left(x+\frac{1}{2}+\frac{3}{2}\right)^2\)

\(=2\left(x+\frac{1}{2}\right)^2+\frac{9}{2}\ge\frac{9}{2}\)

Dấu \(=\)khi \(x+\frac{1}{2}=0\Leftrightarrow x=-\frac{1}{2}\).

 16x²-2x-3

= 16x²-8x+6x-3

= 8x (2x-1)+3 (2x-1)

= (8x+3) (2x-1)

a) \(4-x=2\left(x-4\right)^2\)

\(\Rightarrow4-x=2\left(x^2-8x+16\right)\)

\(\Rightarrow4-x=2x^2+16x-32=0\)

\(\Rightarrow-2x^2+15x-28=0\)

\(\Rightarrow-2x\left(x-4\right)+7\left(x-4\right)=0\)

\(\Rightarrow\left(x-4\right)\left(-2x+7\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x-4=0\\-2x+7=0\end{cases}}\Rightarrow\orbr{\begin{cases}-2x=-7\\x=4\end{cases}}\Rightarrow\orbr{\begin{cases}x=\frac{7}{2}\\x=4\end{cases}}\)

b) \(\left(x^2+1\right)\left(x-2\right)+2x=4\)

\(\Rightarrow\left(x^2+1\right)\left(x-2\right)+2x-4=0\)

\(\Rightarrow\left(x^2+1\right)\left(x-2\right)+2\left(x-2\right)=0\)

\(\Rightarrow\left(x^2+1+2\right)\left(x-2\right)=0\)

\(\Rightarrow\left(x^2+3\right)\left(x-2\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x^2+3=0\\x-2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x^2=-3\text{(Không thoả mãn)}\\x=2\end{cases}}\)

ta có :