Lời giải:
Nếu thêm vào số trừ 19 đơn vị thì hiệu khi đó là:
$456-19=437$

437 nhé 

Lời giải:

a.

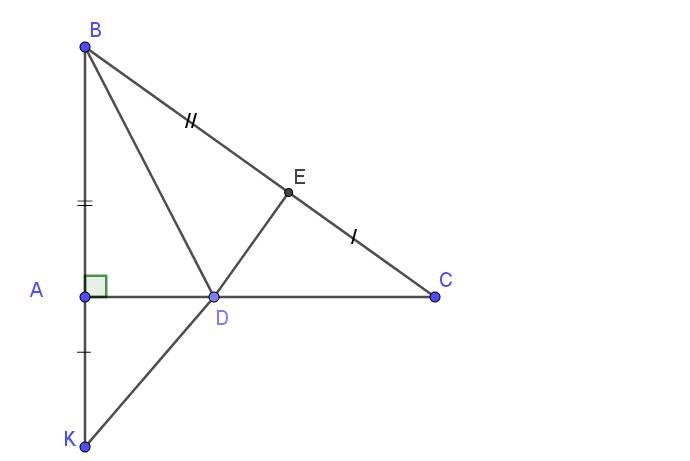
Xét tam giác $ABD$ và $EBD$ có:

$BD$ chung

$AB=EB$ (gt)

$\widehat{ABD}=\widehat{EBD}$ (do $BD$ là phân giác $\widehat{B}$)

$\Rightarrow \triangle ABD=\triangle EBD$ (c.g.c)

b.

Từ tam giác bằng nhau phần a $\Rightarrow \widehat{DEB}=\widehat{DAB}=90^0$

c.

Từ tam giác bằng nhau phần a suy ra $DE=DA(1)$

Từ $\widehat{DEB}=90^0$ suy ra $DE\perp BC$

$\Rightarrow \widehat{DEC}=90^0\Rightarrow \triangle DEC$ vuông tại $E$

$\Rightarrow DE< DC(2)$ (trong tam giác vuông cạnh huyền là cạnh lớn nhất) 

Từ $(1); (2)\Rightarrow DA< DC$

d.

Xét tam giác $DAK$ và $DEC$ có:

$DA=DE$ (cmt)

$\widehat{DAK}=\widehat{DEC}=90^0$

$AK=EC$ (gt)

$\Rightarrow \triangle DAK=\triangle DEC$ (c.g.c)

$\Rightarrow \widehat{ADK}=\widehat{EDC}$

$\Rightarrow \widehat{ADK}+\widehat{ADE}=\widehat{EDC}+\widehat{ADE}$

$\Rightarrow \widehat{KDE}=\widehat{ADC}=180^0$

$\Rightarrow K,E,D$ thẳng hàng.

Hình vẽ:

Lời giải:

Bổ sung đk $x,y,z\geq 0$

Áp dụng BĐT Cauchy-Schwarz:

$\frac{1}{1+xy}+\frac{1}{1+yz}+\frac{1}{1+xz}\geq \frac{9}{1+xy+1+yz+1+xz}=\frac{9}{xy+yz+xz+3}\geq \frac{9}{3+3}=\frac{3}{2}$

Ta có đpcm

Dấu "=" xảy ra khi $x=y=z=1$
 

a: Trên tia Ox, ta có: OB<OA

nên B nằm giữa O và A

=>OB+BA=OA

=>BA+3=7

=>BA=4(cm)

b: Trên tia Ox, ta có: OC<OA

nên C nằm giữa O và A

=>OC+CA=OA

=>CA+5=7

=>CA=2(cm)

Trên tia Ox, ta có: OB<OC

nên B nằm giữa O và C

=>OB+BC=OC

=>BC+3=5

=>BC=2(cm)

Vì BC+CA=BA

nên C nằm giữa B và A

c: Ta có: C nằm giữa B và A

CB=CA(=2cm)

Do đó: C là trung điểm của AB

\(P\left(y\right)\cdot Q\left(y\right)=-2y\left(3y+6\right)\)

\(=-2y\cdot3y-2y\cdot6\)

\(=-6y^2-12y\)

Lời giải:

a.

$M(x)=(-2x^4+2x^4)-0,2x^3+11x^2+5x+7$

$=-0,2x^3+11x^2+5x+7$

Bậc của $M(x)$ là $3$

b.

$C(x)=A(x)+B(x)=(3x^2+3x-18)+(-3x^2-2x+5)$

$=3x^2+3x-18-3x^2-2x+5=(3x^2-3x^2)+(3x-2x)+(-18+5)$

$=x-13$

a: \(M\left(x\right)=7-2x^4+5x-0,2x^3+2x^4+11x^2\)

\(=\left(2x^4-2x^4\right)-0,2x^3+11x^2+5x+7\)

\(=-0,2x^3+11x^2+5x+7\)

bậc là 3

b: C(x)=A(x)+B(x)

\(=3x^2+3x-18-3x^2-2x+5\)

=x-13

Lời giải:

$L(x)=x^2-12x+35=0$

$\Rightarrow (x^2-5x)-(7x-35)=0$

$\Rightarrow x(x-5)-7(x-5)=0$

$\Rightarrow (x-5)(x-7)=0$

$\Rightarrow x-5=0$ hoặc $x-7=0$

$\Rightarrow x=5$ hoặc $x=7$

Vậy $x=5$ và $x=7$ là nghiệm của $L(x)$

- \(x\) - 3\(x^2\) = 0

- \(x\)( 1 + 3\(x\)) =0

\(\left[{}\begin{matrix}x=0\\1+3x=0\end{matrix}\right.\)

\(\left[{}\begin{matrix}x=0\\3x=-1\end{matrix}\right.\)

  \(\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{3}\end{matrix}\right.\)

Vậy \(x\) \(\in\) {0; - \(\dfrac{1}{3}\)}

Lời giải:

$E(x)=-x-3x^2=0$

$\Rightarrow -x(1+3x)=0$

$\Rightarrow x=0$ hoặc $1+3x=0$

$\Rightarrow x=0$ hoặc $x=\frac{-1}{3}$

Vậy nghiệm của $E(x)$ là $x=0$ và $x=\frac{-1}{3}$

13,25:0,5+13,25:0,25+13,25:0,125+13,25:0,2

=13,25x4+13,25x2+13,25x8+13,25x5

=13,25x(4+2+8+5)

=13,25x19

=251,75

45 tạ 15kg=4515kg

Khối lượng muối cửa hàng đã bán được là:

\(4515\times\left(\dfrac{3}{5}+\dfrac{1}{3}\right)=4515\times\dfrac{14}{15}=4214\left(kg\right)\)