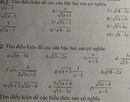Tìm đkxđ của căn thức sau
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



k mk nha
đúng
Bài giải:
Gọi a là độ dài cạnh huyền của tam giác vuông.
Theo định lí Pitago ta có:
a2 = 72 + 242 = 49 + 576 = 625
Nên a = 25cm
Trung tuyến ứng với cạnh huyền có độ dài bằng nửa độ dài cạnh huyền. Nên trung tuyến ứng với cạnh huyền có độ dài là 12,5cm.

ĐKXĐ : \(0\ne x\le1\)
P/t đã cho \(\Leftrightarrow\frac{1}{x}-1-\sqrt{1-x}=0\)
\(\Leftrightarrow\frac{1-x}{x}-\sqrt{1-x}=0\)
\(\Leftrightarrow\sqrt{1-x}\left(\frac{\sqrt{1-x}}{x}-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\sqrt{1-x}=0\\\frac{\sqrt{1-x}}{x}=1\end{cases}}\)
Với \(\sqrt{1-x}=0\Leftrightarrow x=1\)
Với \(\frac{\sqrt{1-x}}{x}=1\Leftrightarrow\sqrt{1-x}=x\) \(\Leftrightarrow\hept{\begin{cases}1-x=x^2\\x>0\end{cases}\Leftrightarrow\hept{\begin{cases}x^2+x-1=0\\x>0\end{cases}}}\)
\(\Leftrightarrow x=\frac{-1+\sqrt{5}}{2}\)( t/m ĐKXĐ )
Vậy ...
\(\Leftrightarrow\hept{\begin{cases}\orbr{\begin{cases}x=\frac{-1+\sqrt{5}}{2}\\x=\frac{-1-\sqrt{5}}{2}\end{cases}}\\x>0\end{cases}}\)

Tập xác định: \(D=ℝ\)
\(\sqrt{2x^2-4x+3}+\sqrt{3x^2-6x+7}=2-x^2+2x\)
Đặt \(\left(x-1\right)^2=x^2-2x+1=t\ge0\).
Phương trình ban đầu tương đương với:
\(\sqrt{2t+1}+\sqrt{3t+4}=3-t\)
\(\Leftrightarrow\sqrt{2t+1}-1+\sqrt{3t+4}-2+t=0\)
\(\Leftrightarrow\frac{2t+1-1}{\sqrt{2t+1}+1}+\frac{3t+4-4}{\sqrt{3t+4}+2}+t=0\)
\(\Leftrightarrow t\left(\frac{2}{\sqrt{2t+1}+1}+\frac{3}{\sqrt{3t+4}+2}+1\right)=0\)
\(\Leftrightarrow t=0\left(tm\right)\)
\(\Leftrightarrow\left(x-1\right)^2=0\)
\(\Leftrightarrow x=1\).

A B C H 14
Ta có : \(\frac{HB}{HC}=\frac{1}{4}\)( gt ) \(\Rightarrow HB=\frac{1}{4}HC\)
Xét tam giác ABC vuông tại A, đường cao AH
* Áp dụng hệ thức : \(AH^2=HB.HC\Rightarrow14^2=\frac{1}{4}HC.HC\)
\(\Leftrightarrow\frac{1}{4}HC^2=196\Leftrightarrow HC^2=784\Leftrightarrow HC=28\)cm
Gỉa thiết : \(HB=\frac{1}{4}HC=\frac{1}{4}.28=7\)cm
\(BC=HB+HC=7+28=35\)cm
* Áp dụng hệ thức :
\(AB^2=BH.BC\Rightarrow AB^2=7.35=245\Rightarrow AB=7\sqrt{5}\)cm
* Áp dụng hệ thức :
\(AC^2=CH.BC\Rightarrow AC^2=28.35=980\Rightarrow AC=14\sqrt{5}\)cm
Chu vi tam giác là :
\(BC+AB+AC=7\sqrt{5}+14\sqrt{5}+35=21\sqrt{5}+35\)cm
Bài 3 :
A B C D 20
Ta có : \(\frac{BD}{BC}=\frac{3}{7}\Rightarrow BD=\frac{3}{7}BC=\frac{3}{7}.20=\frac{60}{7}\)cm
\(\Rightarrow CD=20-\frac{60}{7}=\frac{80}{7}\)cm
Vì AD là đường phân giác nên : \(\frac{AB}{AC}=\frac{BD}{DC}\Rightarrow AB=\frac{\frac{60}{7}}{\frac{80}{7}}AC=\frac{3}{4}AC\)
Áp dụng định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\Rightarrow400=\left(\frac{3}{4}AC\right)^2+AC^2\)
bạn tự giải phương trình này nhé
\(\Rightarrow AC=16\)cm
\(\Rightarrow AB=\frac{3}{4}AC=\frac{3}{4}.16=\frac{48}{4}=12\)cm


o)\(\frac{2\sqrt{3x+4}}{\sqrt{15-3x}}\)có nghĩa \(\Leftrightarrow\hept{\begin{cases}3x+4\ge0\\15-3x>0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ge-\frac{4}{3}\\x< 5\end{cases}}\)\(\Leftrightarrow-\frac{4}{3}\le x< 5\)
f)\(\sqrt{x}.\frac{x}{2\sqrt{3x-5}}\)có nghĩa \(\Leftrightarrow\hept{\begin{cases}x\ge0\\3x-5>0\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}x\ge0\\x>\frac{5}{3}\end{cases}}\)
Sorry nha ,vừa nãy không đọc kĩ yêu cầu của bạn =))
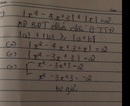

 Giải giúp câu c d
Giải giúp câu c d