chịu

THAM KHẢO NHÉ

Dãy số trên có số số hạng là:

(2468 - 2) : 2 + 1 = 1234 (số)

Từ 2 -> 8 có : 4 CS

Từ 10 -> 98 có: [(98 - 10) : 2 + 1] x 2 = 90 CS

Từ 100 -> 998 có: [(998 - 100) : 2 + 1] x 3 = 1350 CS

Từ 1000 -> 2468 có: [(2468 - 1000) : 2 + 1] x 4 = 2940 CS

Vậy từ 2 đến 2468 có số chữ số là:

4 + 90 + 1350 + 2940 = 4384 (CS)

Tổng các số hạng của dãy trên là:

(2468 + 2) x 1234 : 2 = 1523990

Đề bài chưa đủ dữ liệu em nhé, em thử kiểm tra lại xem mình đã gửi đủ đề bài chưa, thân mến!

Đúng đó, đề bài gì lạ hoắc à

Tỉ số số công nhân tổ một và số công nhân tổ hai là: \(\dfrac{1}{2}\):\(\dfrac{2}{5}\) = \(\dfrac{5}{4}\)

Ta có sơ đồ:  

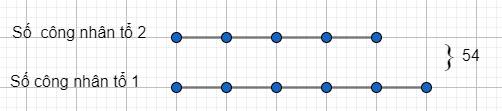
Theo sơ đồ ta có:

Số công nhân tổ 2 là:

54 : ( 4 + 5) \(\times\)4 = 24 (công nhân)

Số công nhân tổ 1 là 54 - 24 = 30 (công nhân)

Đáp số: tổ 1 có 30 công nhân; tổ 2 có 24 công nhân 

a) \(n+18⋮n+1\)

\(\Rightarrow n+18-\left(n+1\right)⋮n+1\)

\(\Rightarrow n+18-n-1⋮n+1\)

\(\Rightarrow17⋮n+1\)

\(\Rightarrow17⋮n+1\)

\(\Rightarrow n+1\in\left\{-1;1;-17;17\right\}\)

\(\Rightarrow n\in\left\{-2;0;-18;16\right\}\left(n\in Z\right)\)

còn ý b nữa bạn

Ba số nguyên liên tiếp có dạng: n; n + 1; n + 2; với n \(\in\) Z

Tổng ba số nguyên liên tiếp là: A =  n + n + 1 + n + 2 = 3n + 3

A = 3.( n + 1)  

với n là số lẻ ta có: n + 1 là số chẵn ⇒ n + 1 ⋮ 2 ⇒ 3.(n + 1) ⋮ 6

Với n là số chẵn ta có: n + 1 là số lẻ ⇒ n + 1 không chia hết cho 2

Khi đó tổng ba số tự nhiên liên tiếp không chia hết cho 6.

Từ những lập luận trên ta có tổng của ba số nguyên liên tiếp không phải lúc nào cũng chia hết cho 6.

Kết luận việc chứng minh tổng ba số nguyên liên tiếp bất kỳ luôn chia hết cho 6 là điều không thể xảy ra. 

`@` `\text {Ans}`

`\downarrow`

`7,`

Ta có:

`2023 = 2024 - 1`

Mà `x = 2024`

`=> 2023 = x - 1`

Thay `2023 = x - 1` vào `f(x)`

`f(x) =`\(x^{15}-\left(x-1\right)x^{14}-\left(x-1\right)x^{13}-...\left(x-1\right)x^2-\left(x-1\right)x-\left(x-1\right)\)

`=`\(x^{15}-x^{15}+x^{14}-x^{14}+x^{13}-...-x^2+x-x+1\)

`=`\(\left(x^{15}-x^{15}\right)+\left(x^{14}-x^{14}\right)+...+\left(x-x\right)+1\)

`= 1`

Vậy, giá trị của `f(x)` khi `x = 2024` là `f(2024) = 1.`

1.

$3x^4-48=3(x^4-16)=3[(x^2)^2-4^2]=3(x^2-4)(x^2+4)$

$=3(x-2)(x+2)(x^2+4)$

2. 

$x^3-4x^2+8x-8=(x^3-8)-(4x^2-8x)$
$=(x-2)(x^2+2x+4)-4x(x-2)=(x-2)(x^2+2x+4-4x)=(x-2)(x^2-2x+4)$

3.

$x^4-27x=x(x^3-27)=x(x^3-3^3)=x(x-3)(x^2+3x+9)$

4.

$x^4-x^3+x^2-1=(x^4-x^3)+(x^2-1)=x^3(x-1)+(x-1)(x+1)$

$=(x-1)(x^3+x+1)$

5.

$x^5+x^3-x^2-1=(x^5+x^3)-(x^2+1)=x^3(x^2+1)-(x^2+1)$
$=(x^2+1)(x^3-1)=(x^2+1)(x-1)(x^2+x+1)$

6.

$x^3+2x^2+2x+1=(x^3+x^2)+(x^2+2x+1)=x^2(x+1)+(x+1)^2$
$=(x+1)(x^2+x+1)$

7.

$x^3+x^2-4x-4=(x^3+x^2)-(4x+4)=x^2(x+1)-4(x+1)$

$=(x+1)(x^2-4)=(x+1)(x-2)(x+2)$

8.

$x^4-2x^3+2x-1=(x^4-2x^3+x^2)-(x^2-2x+1)$

$=(x^2-x)^2-(x-1)^2=x^2(x-1)^2-(x-1)^2=(x-1)^2(x^2-1)=(x-1)^2(x-1)(x+1)$

8¹⁹⁷⁵ = (8⁴)⁴⁹³.8³ = \(\overline{..6}\)⁴⁹³. \(\overline{...2}\) = \(\overline{..2}\)

8^1975=8^1972*8^3

8^1975=(8^4)^493*512

8^1975= ...6^493*512

8^1975=....6*512

=>8^1975=...2