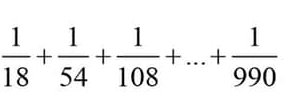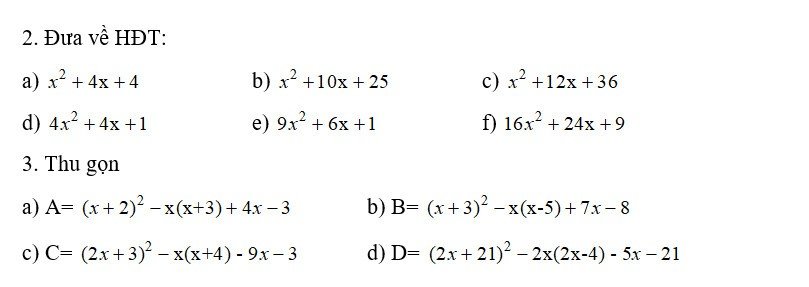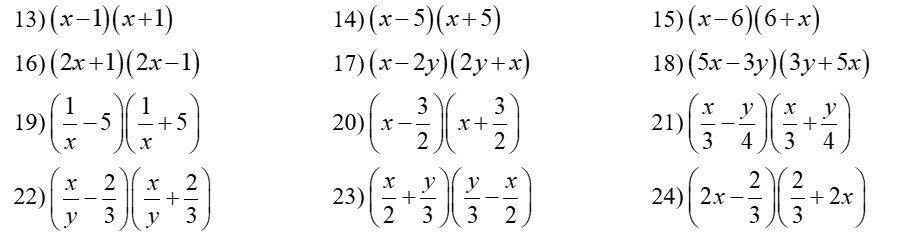
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét ΔABD và ΔAED có
AB=AE
\(\widehat{BAD}=\widehat{EAD}\)
AD chung
Do đó: ΔABD=ΔAED
=>DB=DE
=>D nằm trên đường trung trực của BE(1)
Ta có: AB=AE
=>A nằm trên đường trung trực của BE(2)
Từ (1),(2) suy ra AD là đường trung trực của BE
=>AD\(\perp\)BE

Ta có: I là trung điểm AB =>IC là đường trung tuyến
K là trung điểm của AC =>KB là đường trung tuyến
Vì IC và KB cắt nhau tại H nên H là trực tâm
=> AG là đường trung trực đi qua H
=> A,H,G thẳng hàng

\(\dfrac{1}{18}+\dfrac{1}{54}+\dfrac{1}{108}+...+\dfrac{1}{990}\\ =\dfrac{1}{3\cdot6}+\dfrac{1}{6\cdot9}+...+\dfrac{1}{30\cdot33}\\ =\dfrac{1}{3}\cdot\left(\dfrac{3}{3\cdot6}+\dfrac{3}{6\cdot9}+...+\dfrac{3}{30\cdot33}\right)\\ =\dfrac{1}{3}\cdot\left(\dfrac{1}{3}-\dfrac{1}{6}+\dfrac{1}{6}-\dfrac{1}{9}+...+\dfrac{1}{30}-\dfrac{1}{33}\right)\\ =\dfrac{1}{3}\cdot\left(\dfrac{1}{3}-\dfrac{1}{33}\right)\\ =\dfrac{1}{3}\cdot\dfrac{11-1}{33}\\ =\dfrac{10}{99}\)


2:
a: \(x^2+4x+4=x^2+2\cdot x\cdot2+2^2=\left(x+2\right)^2\)
b: \(x^2+10x+25=x^2+2\cdot x\cdot5+5^2=\left(x+5\right)^2\)
c: \(x^2+12x+36=x^2+2\cdot x\cdot6+6^2=\left(x+6\right)^2\)
d: \(4x^2+4x+1=\left(2x\right)^2+2\cdot2x\cdot1+1^2=\left(2x+1\right)^2\)
e: \(9x^2+6x+1=\left(3x\right)^2+2\cdot3x\cdot1+1^2=\left(3x+1\right)^2\)
f: \(16x^2+24x+9=\left(4x\right)^2+2\cdot4x\cdot3+3^2=\left(4x+3\right)^2\)
3:
a: \(A=\left(x+2\right)^2-x\left(x+3\right)+4x-3\)
\(=x^2+4x+4-x^2-3x+4x-3\)
=5x+1
b: \(B=\left(x+3\right)^2-x\left(x-5\right)+7x-8\)
\(=x^2+6x+9-x^2+5x+7x-8\)
=18x+1
c: \(C=\left(2x+3\right)^2-x\left(x+4\right)-9x-3\)
\(=4x^2+12x+9-x^2-4x-9x-3\)
\(=3x^2-x+6\)
d: \(D=\left(2x+21\right)^2-2x\left(2x-4\right)-5x-21\)
\(=4x^2+84x+441-4x^2+8x-5x-21\)
=87x+420
2:
\(a.x^2+4x+4=x^2+2\cdot x\cdot2+2^2=\left(x+2\right)^2\\ b.x^2+10x+25=x^2+2\cdot x\cdot5+5^2=\left(x+5\right)^2\\ c.x^2+12x+36=x^2+2\cdot x\cdot6+6^2=\left(x+6\right)^2\\ d.4x^2+4x+1=\left(2x\right)^2+2\cdot2x\cdot1+1^2=\left(2x+1\right)^2\\ e.9x^2+6x+1=\left(3x\right)^2+2\cdot3x\cdot1+1^2=\left(3x+1\right)^2\\ f.16x^2+24x+9=\left(4x\right)^2+2\cdot4x\cdot3+3^2=\left(4x+3\right)^2\)

a: \(\left(2x-1\right)^4=81\)
=>\(\left[{}\begin{matrix}2x-1=3\\2x-1=-3\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=4\\2x=-2\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)
b:Sửa đề: \(\left(x-1\right)^5=-32\)
=>\(\left(x-1\right)^5=\left(-2\right)^5\)
=>x-1=-2
=>x=-1
c: \(\left(2x-1\right)^6=\left(2x-1\right)^8\)
=>\(\left(2x-1\right)^8-\left(2x-1\right)^6=0\)
=>\(\left(2x-1\right)^6\left[\left(2x-1\right)^2-1\right]=0\)
=>\(\left(2x-1\right)^6\cdot\left(2x-1-1\right)\cdot\left(2x-1+1\right)=0\)
=>\(2x\left(2x-1\right)^6\cdot\left(2x-2\right)=0\)
=>\(\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=1\end{matrix}\right.\)
a)
\(\left(2x-1\right)^4=81\\ \Rightarrow\left(2x-1\right)^4=3^4\)
TH1: 2x - 1 = 3 => 2x = 4 => x = 2
TH2: 2x - 1 = -3 => 2x = -3 + 1 = -2 => x = -1
b)
\(\left(x-1\right)^5=-32\\ \Rightarrow\left(x-1\right)^5=\left(-2\right)^5\\ \Rightarrow x-1=-2\\ \Rightarrow x=-2+1\\ \Rightarrow x=-1\)
c)
\(\left(2x-1\right)^6=\left(2x-1\right)^8\\ \Rightarrow\left(2x-1\right)^8-\left(2x-1\right)^6=0\\\Rightarrow \left(2x-1\right)^6\left[\left(2x-1\right)^2-1\right]=0\)
TH1:
\(\left(2x-1\right)^6=0\\ \Rightarrow2x-1=0\\ \Rightarrow2x=1\\ \Rightarrow x=\dfrac{1}{2}\)
TH2:
\(\left(2x-1\right)^2-1=0\\ \Rightarrow\left(2x-1\right)^2=1\\ \Rightarrow\left(2x-1\right)^2=1^2\)
+) 2x - 1 = 1 => 2x = 2 => x = 1
+) 2x - 1 = -1 => 2x = 0 => x = 0

1: \(\left(x+1\right)^2=x^2+2\cdot x\cdot1+1^2=x^2+2x+1\)
2: \(\left(4+x\right)^2=4^2+2\cdot4\cdot x+x^2=16+8x+x^2\)
5: \(\left(5x+1\right)^2=\left(5x\right)^2+2\cdot5x\cdot1+1^2=25x^2+10x+1\)
6: \(\left(2x+3\right)^2=\left(2x\right)^2+2\cdot2x\cdot3+3^2=4x^2+12x+9\)
9: \(\left(x+2y\right)^2=x^2+2\cdot x\cdot2y+\left(2y\right)^2=x^2+4xy+4y^2\)
10: \(\left(x+5y\right)^2=x^2+2\cdot x\cdot5y+\left(5y\right)^2=x^2+10xy+25y^2\)
13: \(\left(3x+5y\right)^2=\left(3x\right)^2+2\cdot3x\cdot5y+\left(5y\right)^2\)
\(=9x^2+30xy+25y^2\)
14: \(\left(2x+3y\right)^2=\left(2x\right)^2+2\cdot2x\cdot3y+\left(3y\right)^2\)
\(=4x^2+12xy+9y^2\)
17: \(\left(x^2+9\right)^2=\left(x^2\right)^2+2\cdot x^2\cdot9+9^2=x^4+18x^2+81\)
18: \(\left(2x^2+1\right)^2=\left(2x^2\right)^2+2\cdot2x^2\cdot1+1^2=4x^4+4x^2+1\)
21: \(\left(x+2y^2\right)^2=x^2+2\cdot x\cdot2y^2+\left(2y^2\right)^2=x^2+4xy^2+4y^4\)
22: \(\left(2x+3y^2\right)^2\)
\(=\left(2x\right)^2+2\cdot2x\cdot3y^2+\left(3y^2\right)^2\)
\(=4x^2+12xy^2+9y^4\)

13: \(\left(x-1\right)\left(x+1\right)=x^2+x-x-1=x^2-1\)
14: \(\left(x-5\right)\left(x+5\right)=x^2+5x-5x-25=x^2-25\)
15: \(\left(x-6\right)\left(6+x\right)\)
=(x-6)(x+6)
\(=x^2+6x-6x-36=x^2-36\)
16: \(\left(2x+1\right)\left(2x-1\right)=4x^2-2x+2x-1=4x^2-1\)
17: \(\left(x-2y\right)\left(x+2y\right)=x^2+2xy-2xy-4y^2=x^2-4y^2\)
18: \(\left(5x-3y\right)\cdot\left(3y+5x\right)\)
\(=\left(5x-3y\right)\left(5x+3y\right)\)
\(=25x^2+15xy-15xy-9y^2=25x^2-9y^2\)
19: \(\left(\dfrac{1}{x}-5\right)\left(\dfrac{1}{x}+5\right)=\left(\dfrac{1}{x}\right)^2+\dfrac{5}{x}-\dfrac{5}{x}-25=\dfrac{1}{x^2}-25\)
20: \(\left(x-\dfrac{3}{2}\right)\left(x+\dfrac{3}{2}\right)=x^2+\dfrac{3}{2}x-\dfrac{3}{2}x-\dfrac{9}{4}=x^2-\dfrac{9}{4}\)
21: \(\left(\dfrac{x}{3}-\dfrac{y}{4}\right)\left(\dfrac{x}{3}+\dfrac{y}{4}\right)=\left(\dfrac{x}{3}\right)^2+\dfrac{xy}{12}-\dfrac{xy}{12}-\left(\dfrac{y}{4}\right)^2\)
\(=\dfrac{x^2}{9}-\dfrac{y^2}{16}\)
22: \(\left(\dfrac{x}{y}-\dfrac{2}{3}\right)\left(\dfrac{x}{y}+\dfrac{2}{3}\right)=\left(\dfrac{x}{y}\right)^2+\dfrac{2}{3}\cdot\dfrac{x}{y}-\dfrac{2}{3}\cdot\dfrac{x}{y}-\left(\dfrac{2}{3}\right)^2\)
\(=\left(\dfrac{x}{y}\right)^2-\left(\dfrac{2}{3}\right)^2=\dfrac{x^2}{y^2}-\dfrac{4}{9}\)
23: \(\left(\dfrac{x}{2}+\dfrac{y}{3}\right)\left(\dfrac{y}{3}-\dfrac{x}{2}\right)=\left(\dfrac{y}{3}+\dfrac{x}{2}\right)\left(\dfrac{y}{3}-\dfrac{x}{2}\right)\)
\(=\left(\dfrac{y}{3}\right)^2-\dfrac{x}{2}\cdot\dfrac{y}{3}+\dfrac{x}{2}\cdot\dfrac{y}{3}-\left(\dfrac{x}{2}\right)^2\)
\(=\left(\dfrac{y}{3}\right)^2-\left(\dfrac{x}{2}\right)^2=\dfrac{y^2}{9}-\dfrac{x^2}{4}\)
24: \(\left(2x-\dfrac{2}{3}\right)\left(\dfrac{2}{3}+2x\right)=\left(2x-\dfrac{2}{3}\right)\left(2x+\dfrac{2}{3}\right)\)
\(=4x^2+\dfrac{4}{3}x-\dfrac{4}{3}x-\dfrac{4}{9}=4x^2-\dfrac{4}{9}\)

a, 3.27.9
= 3.33.32
= 31+3+2
= 34+2
= 36
b; 25.5.125
= 52.51.53
= 52+1+3
= 53+3
= 56
c; 49.7.343
= 72.71.73
= 72+1+3
= 73+3
= 76
d; \(\dfrac{2}{3}\).\(\dfrac{4}{9}\).\(\dfrac{8}{27}\)
= \(\left(\dfrac{2}{3}\right)\)1.\(\left(\dfrac{2}{3}\right)\)2.\(\left(\dfrac{2}{3}\right)\)3
= \(\left(\dfrac{2}{3}\right)\)1+2+3
= \(\left(\dfrac{2}{3}\right)\)3+3
= \(\left(\dfrac{2}{3}\right)\)6
e; \(\dfrac{3}{4}\).\(\dfrac{9}{16}\).\(\dfrac{27}{64}\)
= \(\left(\dfrac{3}{4}\right)\)1.\(\left(\dfrac{3}{4}\right)\)2.\(\left(\dfrac{3}{4}\right)\)3
= \(\left(\dfrac{3}{4}\right)\)1+2+3
= \(\left(\dfrac{3}{4}\right)\)3+3
= \(\left(\dfrac{3}{4}\right)\)6
f; \(\dfrac{2}{3}\).\(\dfrac{8}{27}\).\(\dfrac{16}{81}\)
= \(\left(\dfrac{2}{3}\right)\)1.\(\left(\dfrac{2}{3}\right)\)3.\(\left(\dfrac{2}{3}\right)\)4
= \(\left(\dfrac{2}{3}\right)\)1+3+4
= \(\left(\dfrac{2}{3}\right)\)4+4
= \(\left(\dfrac{2}{3}\right)\)8