(\(\sqrt{24}-\sqrt{48}-\sqrt{6}\)).\(\sqrt{6}+12\sqrt{2}\)
Giúp tôi với
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Để hàm số y = (2m - 3)x - 1 // với đường thẳng y = -5x + 3
<=> \(\hept{\begin{cases}2m-3=-5\\-1\ne3\end{cases}}\)<=> 2m = -2 <=> m = -1
b) Hàm số y = (2m - 3)x - 1 đi qua điểm A(-1; 0) => x = -1 và y = 0
Do đó: 0 = (2m - 3).(-1) - 1 = 0 <=> 3 - 2m = 1 <=> 2m = 2 <=> m = 1
Vậy để đò thị hàm số đi qua A(-1; 0) <=> m = 0
c) Gọi tọa độ gđ của 3 đường thẳng y = (2m- 3 )x - 1 , y = 1 và y = 2x - 5 là (x0; y0)
Do đó: \(\hept{\begin{cases}y_0=\left(2m-3\right)x_0-1\\y_0=1\\y_0=2x_0-5\end{cases}}\) <=> \(\hept{\begin{cases}1=\left(2m-3\right)x_0-1\\2x_0-5=1\end{cases}}\)
<=> \(\hept{\begin{cases}\left(2m-3\right)x_0=2\\2x_0=6\end{cases}}\) <=> \(\hept{\begin{cases}\left(2m-3\right).3=2\\x_0=3\end{cases}}\) <=> 2m - 3 = 2/3 <=> 2m = 11/3 <=> m = 11/6
Vậy m = 11/6 thì đồ thị hàm số đã cho và các đường thẳng y = 0 và y = 2x - 5 đồng quy tại 1 điểm

\(\sqrt{13}< \sqrt{153}\)
\(4\sqrt{10}=2\sqrt{4.10}=2\sqrt{40}\)
\(\sqrt{2015}-\sqrt{2014}=\frac{1}{\sqrt{2015}+\sqrt{2014}}\) ; \(\sqrt{2017}-\sqrt{2016}=\frac{1}{\sqrt{2016}+\sqrt{2017}}\)
Suy ra : \(\sqrt{2015}-\sqrt{2014}>\sqrt{2017}-\sqrt{2016}\)


\(\left(5\sqrt{8}-2\sqrt{18}+3\sqrt{50}\right)\left(2\sqrt{6}-3\sqrt{10}\right)\)
\(=\left(10\sqrt{2}-6\sqrt{2}+15\sqrt{2}\right)\left(2\sqrt{6}-3\sqrt{10}\right)\)
\(=19\sqrt{2}\left(2\sqrt{6}-3\sqrt{10}\right)=76\sqrt{3}-114\sqrt{5}\)


ĐK: \(x>0,x\ne1\).
\(P=\frac{x^2-\sqrt{x}}{x+\sqrt{x}+1}-\frac{2x+\sqrt{x}}{\sqrt{x}}+\frac{2\left(x-1\right)}{\sqrt{x}-1}\)
\(=\frac{\sqrt{x}\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}{x+\sqrt{x}+1}-\frac{\sqrt{x}\left(2\sqrt{x}+1\right)}{\sqrt{x}}+\frac{2\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{\sqrt{x}-1}\)
\(=x-\sqrt{x}-2\sqrt{x}-1+2\sqrt{x}+2\)
\(=x-\sqrt{x}+1\)
\(x-\sqrt{x}+1=x-\sqrt{x}+\frac{1}{4}+\frac{3}{4}=\left(\sqrt{x}-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Dấu \(=\)khi \(x=\frac{1}{4}\).
\(Q=\frac{2\sqrt{x}}{x-\sqrt{x}+1}\Rightarrow Qx-Q\sqrt{x}+Q=2\sqrt{x}\)
\(\Leftrightarrow Qx-\sqrt{x}\left(Q+2\right)+Q=0\)
Với \(Q=0\Rightarrow x=0\)không thỏa mãn.
Với \(Q\ne0\):
Đặt \(\sqrt{x}=t>0\).
\(Qt^2-t\left(Q+2\right)+Q=0\)
\(\Delta=\left(Q+2\right)^2-4Q^2=-3Q^2+4Q+4\)
Phương trình có nghiệm suy ra \(-3Q^2+4Q+4\ge0\Leftrightarrow-\frac{2}{3}\le Q\le2\)
mà \(Q\inℤ\)\(\Rightarrow Q\in\left\{0,1,2\right\}\).
Với từng giá trị \(Q\)ta thế trực tiếp tìm giá trị của \(x\).
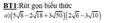
\(\left(\sqrt{24}-\sqrt{48}-\sqrt{6}\right)\sqrt{6}+12\sqrt{2}=\left(2\sqrt{6}-4\sqrt{3}-\sqrt{6}\right)\sqrt{6}+12\sqrt{2}\)
\(=12-12\sqrt{2}-6+12\sqrt{2}=6\)
\(\left(\sqrt{24}-\sqrt{48}-\sqrt{6}\right)\sqrt{6}+12\sqrt{2}\)
\(=\sqrt{24.6}-\sqrt{48.6}-6+12\sqrt{2}\)
\(=\sqrt{144}-\sqrt{288}-6+12\sqrt{2}\)
\(=12-12\sqrt{2}-6+12\sqrt{2}\)
\(=6\)