Ai giup toi bai nay voi kho qua
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Áp dụng BĐT Cauchy - Shwarz ta có :
\(B=\frac{1}{a}+\frac{1}{b}\ge\frac{\left(1+1\right)^2}{a+b}=\frac{4}{3}\)
Dấu ''='' xảy ra khi \(a=b=\frac{3}{2}\)

a, \(\sqrt{x^2-2x+1}=5\Leftrightarrow\left|x-1\right|=5\)
TH1 : \(x-1=5\Leftrightarrow x=6\)
TH2 : \(x-1=-5\Leftrightarrow x=-4\)
b, \(\sqrt{9x^2-6x+1}=2x-3\Leftrightarrow\left|3x-1\right|=2x-3\)
ĐK : \(x\ge\frac{3}{2}\)
TH1 : \(3x-1=2x-3\Leftrightarrow x=-2\)( ktm )
TH2 : \(3x-1=3x-2\Leftrightarrow0x=-1\)( ktm )
Vậy pt vô nghiệm
c, \(\sqrt{9x^2}=2x+1\Leftrightarrow\left|3x\right|=2x+1\)
ĐK : \(x\ge-\frac{1}{2}\)
TH1 : \(3x=2x+1\Leftrightarrow x=1\)
TH2 : \(3x=-2x-1\Leftrightarrow5x=-1\Leftrightarrow x=-\frac{1}{5}\)

\(a,\sqrt{x^2-2x+1}=5\)
\(\sqrt{\left(x-1\right)^2}=5\)
\(\left|x-1\right|=5\)
\(\orbr{\begin{cases}x-1=5\\x-1=-5\end{cases}\orbr{\begin{cases}x=6\left(TM\right)\\x=-4\left(TM\right)\end{cases}}}\)
\(b,\sqrt{9x^2-6x+1}=2x-3\)
\(\sqrt{\left(3x-1\right)^2}=2x-3\)
\(\left|3x-1\right|=2x-3\)
\(\orbr{\begin{cases}3x-1=2x-3\\3x-1=3-2x\end{cases}\orbr{\begin{cases}x=-2\left(TM\right)\\x=\frac{4}{5}\left(TM\right)\end{cases}}}\)
\(c,\sqrt{9x^2}=2x+1\)
\(\left|3x\right|=2x+1\)
\(\orbr{\begin{cases}3x=2x+1\\3x=-2x-1\end{cases}\orbr{\begin{cases}x=1\left(TM\right)\\x=-\frac{1}{5}\left(TM\right)\end{cases}}}\)

\(\left(\sqrt{4-\sqrt{7}}-\sqrt{4+\sqrt{7}}\right)^2\)
\(=4-\sqrt{7}-2\sqrt{16-7}+4+\sqrt{7}=8-2.3=2\)

a, Gọi ptđt (d) có dạng y = ax + b
\(\left(d\right)//y=3x+1\Leftrightarrow\hept{\begin{cases}a=3\\b\ne1\end{cases}}\)
đt (d) đi qua A(3;7) <=> \(7=3a+b\)(*)
Thay a = 3 vào (*) ta được : \(9+b=7\Leftrightarrow b=-2\)( tmđk )
Vậy ptđt có dạng y = 3x - 2
b, Hoành độ giao điểm thỏa mãn phương trình
\(x^2=3x-2\Leftrightarrow x^2-3x+2=0\Leftrightarrow\left(x-1\right)\left(x-2\right)=0\Leftrightarrow x=1;x=2\)
\(\Rightarrow y=1;y=4\)
Vậy (d) cắt (P) tại A( 1;1 ) ; B( 2 ; 4 )
a, Phương trình đường thẳng (d) là: y = ax + b
Vì đường thẳng (d) song song với đường thẳng y = 3x + 1 nên
⇒⇒ {a=a′b≠b′{a=a′b≠b′ ⇔⇔ {a=3b≠1{a=3b≠1
Với a = 3 ta được pt đường thẳng (d): y = 3x + b
Vì đường thẳng (d) đi qua điểm A(3;7) nên thay x = 3; y = 7 ta được:
7 = 3.3 + b
⇔⇔ b = -2 (TM)
Vậy phương trình đường thẳng (d) là: y = 3x - 2
Chúc bn học tốt!
k mình nha


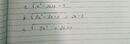

bạn đăng tách câu hỏi ra cho mn cùng giúp nhé
Bài 4 :
\(A=3x+\sqrt{16-24x+9x^2}=3x+\sqrt{\left(4-3x\right)^2}=3x+\left|3x-4\right|\)
Thay x = -3 vào A ta được : \(=-9+\left|-13\right|=-9+13=4\)
\(B=5x-\sqrt{4x^2+12x+9}=5x-\sqrt{\left(2x+3\right)^2}=5x-\left|2x+3\right|\)
Thay x = -\(\sqrt{5}\)vào B ta được : \(=-5\sqrt{5}-\left|-2\sqrt{5}+3\right|\)
\(=-5\sqrt{5}+2\sqrt{5}-3=-3\sqrt{5}-3\)
Bài 5
a, \(\left(3+\sqrt{5}\right)\left(3-\sqrt{5}\right)-\left(2+\sqrt{3}\right)\left(2-\sqrt{3}\right)=3\)
\(VT=9-5-\left(4-3\right)==4-1=3=VP\)
Vậy ta có đpcm
b, \(2\sqrt{3}\left(\sqrt{3}-1\right)+\left(2-\sqrt{3}\right)^2+6\sqrt{3}=13\)
\(VT=2.3-2\sqrt{3}+4-4\sqrt{3}+3+6\sqrt{3}=6-2\sqrt{3}+7-4\sqrt{3}+6\sqrt{3}\)
\(=13=VP\)Vậy ta có đpcm