x(x-5)-x+5=0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(2x\left(1-7x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{1}{7}\end{matrix}\right.\)

\(\left(2024^2+2022^2+2020^2+...+2^2\right)-\left(2023^2+2021^2+2019^2+...+1^2\right)\\ =\left(2024^2-2023^2\right)+\left(2022^2-2021^2\right)+\left(2020^2-2019^2\right)+...+\left(2^2-1^2\right)\\ =\left(2024-2023\right)\left(2024+2023\right)+\left(2022-2021\right)\left(2022+2021\right)+\left(2020-2019\right)\left(2020+2019\right)+...+\left(2-1\right)\left(2+1\right)\)\(=1.\left(2024+2023\right)+1.\left(2022+2021\right)+1.\left(2020+2019\right)+...+1.\left(2+1\right)\)\(=1+2+...+2019+2020+2021+2022+2023+2024\)\(=\dfrac{\left(1+2024\right).2024}{2}=2049300\)
\(\left(2024^2+2022^2+2020^2+....+2^2\right)-\left(2023^2+2021^2+.....+1^2\right)\\ =2024^2+2022^2+2020^2+....+2^2-2023^2-2021^2-....-1^2\\ =\left(2024^2-2023^2\right)+\left(2022^2-2021^2\right)+.....+\left(2^2-1^2\right)\\ =\left(2024-2023\right)\cdot\left(2024+2023\right)+\left(2022-2021\right)\cdot\left(2022+2021\right)+.....+\left(2-1\right)\cdot\left(2+1\right)\\ =2024+2023+2022+2021+....+2+1\\ =\left(2024+1\right)\cdot\left[\left(2024-1\right):1+1\right]:2\\ =2025\cdot2024:2\\ =2049300\)

Đáp án + Giải thích các bước giải:
Gọi x ( m ) là chiều dài ban đầu của khu vườn hình chữ nhật ( x∈N∗∗, x > 0 )
Gọi y ( m ) là chiều rộng ban đầu của khu vườn hình chú nhật ( y∈N∗∗ , y > 0 )
Một khu vườn hình chữ nhật có chu vi là 200 m, nên ta có phương trình:
( x + y ) . 2 = 200
⇔ 2x + 2y = 200 ( 1 )
Do mở rộng đường giao thông nông thôn nên chiều dài vườn giảm 8 m và biết diện tích đất còn lại là 2080 cm² dùng để trồng cây, nên ta có phương trình:
( x - 8 ) . y = 2080 ( 2 )
Ta có: ( 1 )
2x + 2y = 200
⇔ x + y = 100
⇔ x = 100 - y
Thay y vào ( 2 ), ta được:
( 100 - y - 8 ) . y = 2080
⇔ 92y - y² = 2080
⇔ - y² + 92y - 2080 = 0
Giải phương trình, ta được:
{y=52y=40{�=52�=40
=> 100 - 52 = 48 ( nhận )
=> 100 - 40 = 60 ( nhận )
Vậy chiều dài là 60 m và chiều rộng là 48 - 8 = 40 m

a: Gọi giá niêm yết của 1 cái bút là x(đồng)
(Điều kiện: x>0)
Giá của 1 cây bút trong 30 cây bút đầu tiên là:
\(x\left(1-20\%\right)=0,8x\left(đồng\right)\)
Giá của 1 cây bút từ cây thứ 31 là:
\(0,8x\cdot\left(1-40\%\right)=0,48x\left(đồng\right)\)
Tổng số tiền là 900000 đồng nên ta có:
\(0,8x\cdot30+0,48x\cdot10=900000\)
=>24x+4,8x=900000
=>28,8x=900000
=>x=31250(nhận)
vậy: Giá niêm yết của 1 cây bút là 31250 đồng
b: Số tiền còn lại sau khi mua 40 cây đầu tiên là:
1260000-900000=360000(đồng)
Số cây bút còn lại mua được là:
360000:(0,48*31250)=24(cây)
Tổng số cây bút mua được là:
40+24=64(cây)

a: Xét ΔAMB vuông tại A và ΔIMA vuông tại I có
\(\widehat{AMB}\) chung
Do đó: ΔAMB~ΔIMA
b: Ta có:ABCD là hình vuông
=>AC\(\perp\)BD tại O, O là trung điểm chung của AC và BD
Xét ΔDOC vuông tại O và ΔDCB vuông tại C có
\(\widehat{ODC}\) chung
DO đó: ΔDOC~ΔDCB
=>\(\dfrac{DC}{DB}=\dfrac{OC}{CB}\)
=>\(DC\cdot CB=OC\cdot DB\)
c: Xét ΔHAB có
BI,AO là các đường cao
BI cắt AO tại K
Do đó: K là trực tâm của ΔHAB
=>HK\(\perp\)AB
mà AB\(\perp\)AD
nên HK//AD
d:
M là trung điểm của AD
=>\(AD=2\cdot AM=60\left(cm\right)\)
=>AB=60(cm)
ΔABM vuông tại A
=>\(BM^2=AB^2+AM^2=60^2+30^2=4500\)
=>\(BM=\sqrt{4500}=30\sqrt{5}\left(cm\right)\)
ΔABM vuông tại A
=>\(S_{ABM}=\dfrac{1}{2}\cdot AB\cdot AM=900\left(cm^2\right)\)
Xét ΔBIA vuông tại I và ΔBAM vuông tại A có
\(\widehat{IBA}\) chung
Do đó ΔBIA~ΔBAM
=>\(\dfrac{S_{BIA}}{S_{BAM}}=\left(\dfrac{BA}{BM}\right)^2=\left(\dfrac{60}{30\sqrt{5}}\right)^2=\left(\dfrac{2}{\sqrt{5}}\right)^2=\dfrac{4}{5}\)
=>\(S_{BIA}=\dfrac{4}{5}\cdot S_{BAM}=720\left(cm^2\right)\)
a/ Xét tg vuông AMB và tg vuông IMA có
ˆMAI=ˆABM���^=���^ (cùng phụ với ˆAMB���^ )
=> tg AMB đồng dạng với tg IMA (g.g.g)
b/
Trong hình vuông hai đường chéo vuông góc với nhau
Xét tg vuông OBC và tg vuông CBD có
ˆDBC���^ chung => tg OBC đồng dạng với tg CBD ⇒OCDC=BCBD⇒OC.BD=BC.DC(dpcm)⇒����=����⇒��.��=��.��(����)
c/ Kéo dài AH cắt CD tại N
Xét tg vuông ABM và tg vuông DAN có
ˆDAN=ˆABM���^=���^ (cùng phụ với ˆAMB���^ )
AB=AD (cạnh hình vuông)
⇒ΔABM=ΔDAN⇒Δ���=Δ��� (Tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)
=> AM=DN mà AM=AD2��=��2 Và AD=CD ⇒DN=AD2=CD2⇒DN=CN⇒��=��2=��2⇒��=��
Xét tg ADC có
OA=OC (trong tg vuông hai đường chéo cắt nhau tại trung điểm mỗi đường) => DO là trung tuyến của tg ADC
DN=CN (cmt) => AN là trung tuyến của tg ADC
=> H là trọng tâm của tg ADC ⇒HODO=13⇒HODH=12⇒HO1=DH2=HO+DH1+2=OD3⇒����=13⇒����=12⇒��1=��2=��+��1+2=��3
Mà OD=OB ⇒DH2=HO1=OB3=HO+OB1+3=BH4⇒DH=BH2⇒BH=2.DH(dpcm)

1: \(\left(2x+1\right)^2-2\left(2x+1\right)\left(3-x\right)+\left(x-3\right)^2\)
\(=\left(2x+1\right)^2+2\left(2x+1\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+1+x-3\right)^2=\left(3x-2\right)^2=9x^2-12x+4\)
2: \(\left(x-1\right)^3-\left(x+1\right)\left(x^2-x+1\right)-\left(1-3x\right)\left(1+3x\right)\)
\(=x^3-3x^2+3x-1-\left(x^3+1\right)-\left(1-9x^2\right)\)
\(=x^3-3x^2+3x-1-x^3-1-1+9x^2\)
\(=6x^2+3x-3\)
3: \(\left(x+2\right)\left(x^2-2x+4\right)-x\left(x-1\right)\left(x+1\right)+3x\)
\(=x^3+8-x\left(x^2-1\right)+3x\)
\(=x^3+8-x^3+x+3x=4x+8\)
4: \(\left(3x-2\right)^2-3\left(x-4\right)\left(x+4\right)+\left(x-3\right)^2-\left(x+1\right)\left(x^2-x+1\right)\)
\(=9x^2-12x+4-3\left(x^2-16\right)+x^2-6x+9-\left(x^3+1\right)\)
\(=10x^2-18x+13-3x^2+48-x^3-1\)
\(=-x^3+7x^2-18x+12\)
5: \(\left(x+1\right)^2-\left(x-1\right)^2-3\left(x-3\right)\left(x+3\right)\)
\(=x^2+2x+1-x^2+2x-1-3\left(x^2-9\right)\)
\(=4x-3x^2+27\)
6: \(\left(x-1\right)^3-x\left(x-2\right)^2+x-1\)
\(=x^3-3x^2+3x-1-x\left(x^2-4x+4\right)+x-1\)
\(=x^3-3x^2+4x-2-x^3+4x^2-4x\)
\(=x^2-2\)
7: \(\left(x+2\right)^3-x^2\left(x+6\right)-8\)
\(=x^3+6x^2+12x+8-x^3-6x^2-8\)
=12x
8: \(\left(x+y\right)^3-\left(x-y\right)^3-2y^3\)
\(=\left(x^3+3x^2y+3xy^2+y^3\right)-\left(x^3-3x^2y+3xy^2-y^3\right)-2y^3\)
\(=x^3+3x^2y+3xy^2+y^3-x^3+3x^2y-3xy^2+y^3-2y^3\)
\(=6x^2y\)
9: \(\left(x-1\right)^3-\left(x+1\right)^3+6\left(x-1\right)\left(x+1\right)\)
\(=x^3-3x^2+3x-1-x^3-3x^2-3x-1+6\left(x^2-1\right)\)
\(=-6x^2-2+6x^2-6=-8\)
10: \(4x\left(3x-5\right)-2\left(4x+1\right)-x-7\)
\(=12x^2-20x-8x-2-x-7\)
\(=12x^2-29x-9\)
11: \(\left(3x+1\right)^2-2\left(3x+1\right)\left(5x+5\right)+\left(5x+5\right)^2\)
\(=\left(5x+5-3x-1\right)^2\)
\(=\left(2x+4\right)^2=4x^2+16x+16\)
12: \(\left(2x+3\right)^2+\left(2x+3\right)\left(2x-6\right)+\left(x-3\right)^2\)
\(=\left(2x+3\right)^2+2\cdot\left(2x+3\right)\left(x-3\right)+\left(x-3\right)^2\)
\(=\left(2x+3+x-3\right)^2=\left(3x\right)^2=9x^2\)
13: \(\left(x^2-2x+4\right)\left(x+2\right)-\left(x+1\right)^3+3\left(x-1\right)\left(x+1\right)\)
\(=x^3+8-x^3-3x^2-3x-1+3\left(x^2-1\right)\)
\(=-3x^2-3x+7+3x^2-3=-3x+4\)
14: \(\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+4\left(x+1\right)^2\)
\(=\left(x-2\right)^2+2\left(x-2\right)\left(2x+2\right)+\left(2x+2\right)^2\)
\(=\left(x-2+2x+2\right)^2=\left(3x\right)^2=9x^2\)

Lời giải:
Áp dụng BĐT Cô-si:
$\frac{x^2+y^2}{4}+\frac{1}{x^2+y^2}\geq 2\sqrt{\frac{x^2+y^2}{4}.\frac{1}{x^2+y^2}}=1$
Áp dụng BĐT Bunhiacopxky:
$\frac{3(x^2+y^2)}{4}=\frac{3(1+1)(x^2+y^2)}{8}\geq \frac{3(x+y)^2}{8}=\frac{3.2^2}{8}=\frac{3}{2}$
$\Rightarrow B\geq 1+\frac{3}{2}=\frac{5}{2}$
Vậy $B_{\min}=\frac{5}{2}$
Giá trị này đạt tại $x=y=1$

Xét tam giác AEB và tam giác CFD ta có
AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt)
Vậy tam giác AEB = tam giác CFD ( c.g.c )
=> AE = FC ( 2 cạnh tương ứng ) (1)
tương tự với tam giác AFD = tam giác EBC
=> AF = EC (2)
Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF
Xét tam giác AEB và tam giác CFD ta có
AB = CD (tứ giác ABCD là hbn); ^ABE = ^CDF ( soletrong ) ; DF = BE (gt)
Vậy tam giác AEB = tam giác CFD ( c.g.c )
=> AE = FC ( 2 cạnh tương ứng ) (1)
tương tự với tam giác AFD = tam giác EBC
=> AF = EC (2)
Từ (1) ; (2) => tứ giác AECF là hbh => AE // CF

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC~ΔHBA
b: ΔABC vuông tại A
=>\(BC^2=AB^2+AC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
ΔABC~ΔHBA
=>\(\dfrac{AB}{HB}=\dfrac{BC}{BA}=\dfrac{AC}{HA}\)
=>\(HA=\dfrac{AB\cdot AC}{BC}=4,8\left(cm\right)\)
c: Xét ΔAHB có AD là phân giác
nên \(\dfrac{DH}{DB}=\dfrac{AH}{AB}\)(1)
Xét ΔCHA vuông tại H và ΔCAB vuông tại A có
\(\widehat{HCA}\) chung
Do đó: ΔCHA~ΔCAB
=>\(\dfrac{CH}{CA}=\dfrac{AH}{AB}\)(2)
Ta có: \(\widehat{CAD}+\widehat{BAD}=\widehat{CAB}=90^0\)
\(\widehat{CDA}+\widehat{HAD}=90^0\)(ΔHAD vuông tại H)
mà \(\widehat{BAD}=\widehat{HAD}\)(AD là phân giác của góc BAH)
nên \(\widehat{CAD}=\widehat{CDA}\)
=>CA=CD(3)
Từ (1),(2),(3) suy ra \(\dfrac{DH}{DB}=\dfrac{HC}{DC}\)
=>\(DH\cdot DC=HC\cdot DB\)

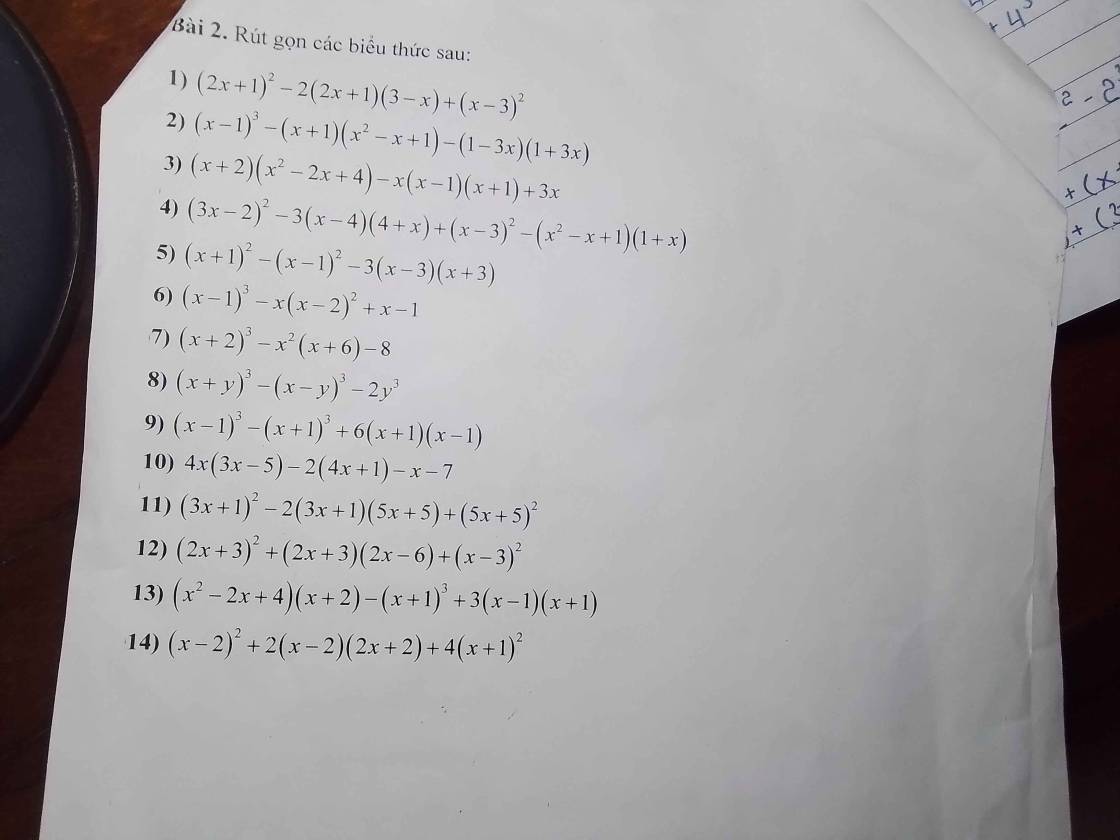

\(x\left(x-5\right)-\left(x-5\right)=0\Leftrightarrow\left(x-1\right)\left(x-5\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=5\end{matrix}\right.\)
X=5;4