Cho L(x) = 0

x² - 12x + 35 = 0

x² - 5x - 7x + 35 = 0

(x² - 5x) - (7x - 35) = 0

x(x - 5) - 7(x - 5) = 0

(x - 5)(x - 7) = 0

x - 5 = 0 hoặc x - 7 = 0

*) x - 5 = 0

x = 5

*) x - 7 = 0

x = 7

Vậy nghiệm của đa thức L(x) là: x = 5; x = 7

Em cần làm gì với đa thức này

s là nam n là bắc

a: Xét ΔCED vuông tại E và ΔCFD vuông tại F có

CD chung

\(\widehat{ECD}=\widehat{FCD}\)

Do đó: ΔCED=ΔCFD

=>CE=CF: DE=DF

Xét ΔCEK vuông tại E và ΔCFH vuông tại F có

CE=CF
\(\widehat{ECK}\) chung

Do đó: ΔCEK=ΔCFH

b: Xét ΔDEH vuông tại E và ΔDFK vuông tại F có

DE=DF

\(\widehat{EDH}=\widehat{FDK}\)

Do đó: ΔDEH=ΔDFK

=>DH=DK 

=>D nằm trên đường trung trực của HK(1)

Ta có: CH=CK

=>C nằm trên đường trung trực của HK(2)

Ta có: MH=MK

=>M nằm trên đường trung trực của HK(3)

Từ (1),(2),(3) suy ra C,D,M thẳng hàng

a: Xét ΔAMB và ΔAMC có

AM chung

MB=MC

AB=AC

Do đó: ΔAMB=ΔAMC

=>\(\widehat{BAM}=\widehat{CAM}\)

Xét ΔAHM vuông tại H và ΔAKM vuông tại K có

AM chung

\(\widehat{HAM}=\widehat{KAM}\)

Do đó: ΔAHM=ΔAKM

=>MH=MK

b: Ta có: MH=MK

mà MK<MC(ΔMKC vuông tại K)

nên MH<MC

c: ΔKAM vuông tại K

=>AM là cạnh lớn nhất trong ΔKAM

=>MK<AM

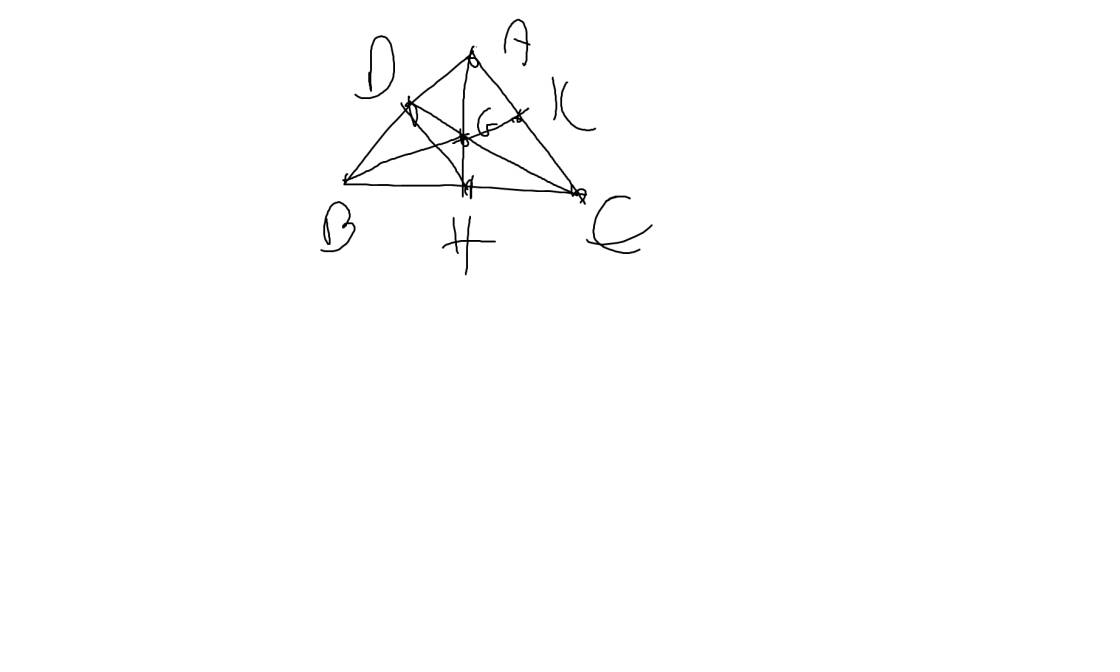
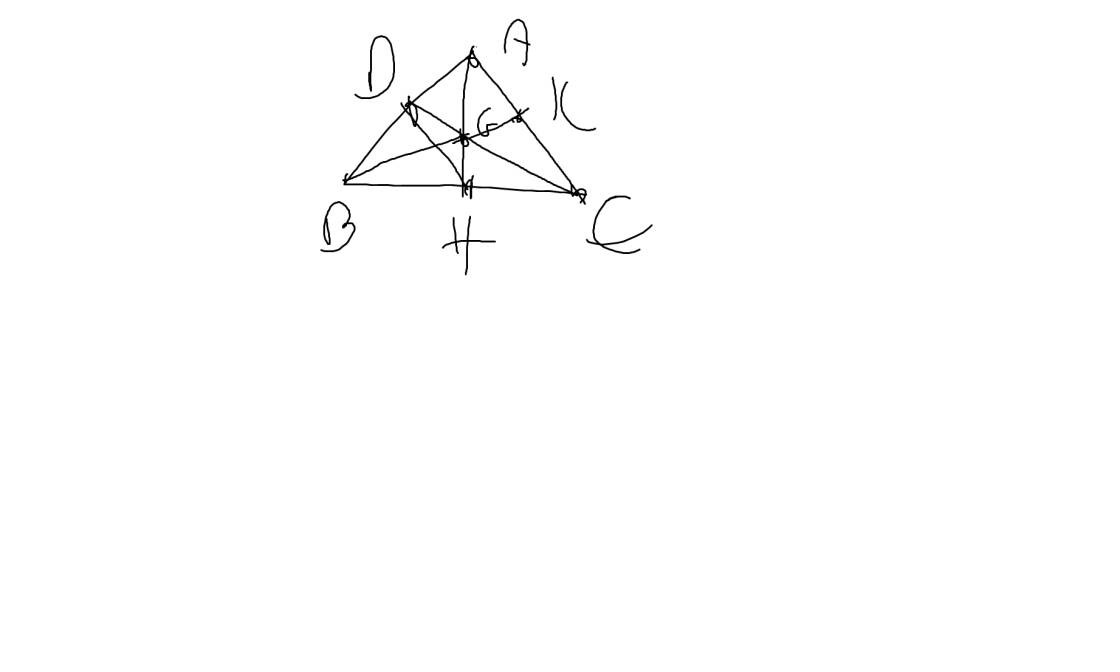
a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)

nên \(\widehat{DHA}=\widehat{DAH}\)

=>ΔDAH cân tại D

b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)

\(\widehat{DAH}+\widehat{DBH}=90^0\)

mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)

nên \(\widehat{DHB}=\widehat{DBH}\)

=>DH=DB

=>DA=DB

=>D là trung điểm của AB

Xét ΔABC có

AH,CD là các đường trung tuyến

AH cắt CD tại G

Do đó: G là trọng tâm của ΔABC

c: Xét ΔABC có

G là trọng tâm

Do đó: BG cắt AC tại trung điểm K của AC

TA có: 

mà AB=AC

nên AD=DB=AK=KC

Xét ΔDBC và ΔKCB có

DB=KC

BC chung

Do đó: ΔDBC=ΔKCB

=>DC=BK

Xét ΔBAC có 

G là trọng tâm

BK là đường trung tuyến

Do đó: 

=>2BK=3BG

Trên tia đối của tia KB, lấy E sao cho KB=KE

Xét ΔKAE và ΔKCB có

KA=KC

(hai góc đối đỉnh)

KE=KB

Do đó: ΔKAE=ΔKCB

=>AE=CB 

AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

a: Xét ΔAHB vuông tại H và ΔAHC vuông tại H có

AB=AC

AH chung

Do đó: ΔAHB=ΔAHC

=>\(\widehat{HAB}=\widehat{HAC}\)

mà \(\widehat{DHA}=\widehat{HAC}\)(DH//AC)

nên \(\widehat{DHA}=\widehat{DAH}\)

=>ΔDAH cân tại D

b: Ta có: \(\widehat{DHA}+\widehat{DHB}=90^0\)

\(\widehat{DAH}+\widehat{DBH}=90^0\)

mà \(\widehat{DHA}=\widehat{DAH}\)(ΔDAH cân tại D)

nên \(\widehat{DHB}=\widehat{DBH}\)

=>DH=DB

=>DA=DB

=>D là trung điểm của AB

Xét ΔABC có

AH,CD là các đường trung tuyến

AH cắt CD tại G

Do đó: G là trọng tâm của ΔABC

c: Xét ΔABC có

G là trọng tâm

Do đó: BG cắt AC tại trung điểm K của AC

TA có: \(AD=DB=\dfrac{AB}{2}\)

\(AK=KC=\dfrac{AC}{2}\)

mà AB=AC

nên AD=DB=AK=KC

Xét ΔDBC và ΔKCB có

DB=KC

\(\widehat{DBC}=\widehat{KCB}\)

BC chung

Do đó: ΔDBC=ΔKCB

=>DC=BK

Xét ΔBAC có 

G là trọng tâm

BK là đường trung tuyến

Do đó: \(\dfrac{BG}{BK}=\dfrac{2}{3}\)

=>2BK=3BG

Trên tia đối của tia KB, lấy E sao cho KB=KE

Xét ΔKAE và ΔKCB có

KA=KC

\(\widehat{AKE}=\widehat{CKB}\)(hai góc đối đỉnh)

KE=KB

Do đó: ΔKAE=ΔKCB

=>AE=CB 

AH+3BG=AH+2BK=AH+BE<AB+BE<(AB+AE+AB)=AB+AC+BC

a) Góc EAF là góc giữa hai đường trung trực của AB và AC. Do đó, góc EAF sẽ bằng 180o - góc A = 180^o - 100^o = 80^o.

b) Để chứng minh AO là tia phân giác của góc EAF, ta cần chứng minh rằng góc EAO = góc FAO.

Ta biết rằng góc EAO = góc BAO = \(\dfrac{1}{2}\) góc BAC = \(\dfrac{1}{2}\cdot\) 100^o = 50^o (vì AO là đường trung trực của AB).
Tương tự, góc FAO = góc CAO = \(\dfrac{1}{2}\) góc CAB = \(\dfrac{1}{2}\cdot\) 100^o = 50^o (vì AO là đường trung trực của AC).
Vì góc EAO = góc FAO, nên AO là tia phân giác của góc EAF.

hơi sai sai

a ) - Bạn Thiện làm việc sai

     - Vì bạn ấy chen lấn hàng của người có hoàn cảnh.

b ) - Em sẽ khuyên bạn để bạn hiểu ra vấn đề .

a. Việc làm của bạn Thiện sai vì:

- Không tôn trọng người khác.

- Thiếu văn hoá khi chen hàng..

b. Nếu em là Thiện, em sẽ nhắc nhở bạn ấy việc làm của bạn là sai, thiếu văn hoá, và kéo bạn ấy về xếp hàng. Trước đó cần xin lỗi chú khiếm thị vì đã thiếu tôn trọng chú.