
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Định lí Talet trong hình thang
Nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.

a) Ta sẽ chứng minh
A≥13A≥13 (@)
⇔x2−x+1x2+x+1≥13⇔x2-x+1x2+x+1≥13
⇔x2−x+1x2+x+1−13≥0⇔x2-x+1x2+x+1-13≥0
⇔3x2−3x+3−x2−x−13(x2+x+1)≥0⇔3x2-3x+3-x2-x-13(x2+x+1)≥0
Ta có : x(x+1)≥0∀xx(x+1)≥0∀x (hai số liên tiếp)
⇒x2+x+1≥0∀x⇒x2+x+1≥0∀x
⇒3(x2+x+1)≥0∀x⇒3(x2+x+1)≥0∀x
⇒A≥13⇔3x2−3x+3−x2−x−1≥0⇒A≥13⇔3x2-3x+3-x2-x-1≥0
⇔2x2−4x+2≥0⇔2x2-4x+2≥0
⇔2(x−1)2≥0⇔2(x-1)2≥0 (@@)
Ta có : @@ đúng ∀x∀x
⇒ @ đúng ∀x∀x
⇒GTNN của A=13A=13 đạt khi x=1x=1
b) Ta sẽ chứng minh
A≤3A≤3 (#)
⇔x2−x+1x2+x+1≤3⇔x2-x+1x2+x+1≤3
⇔x2−x+1x2+x+1−3≤0⇔x2-x+1x2+x+1-3≤0
⇔x2−x+1−3x2−3x−3x2+x+1≤0⇔x2-x+1-3x2-3x-3x2+x+1≤0
Ta có : x(x+1)≥0∀xx(x+1)≥0∀x (hai số liên tiếp)
⇒x2+x+1≥0∀x⇒x2+x+1≥0∀x
⇒A≤3⇔x2−x+1−3x2−3x−3≤0⇒A≤3⇔x2-x+1-3x2-3x-3≤0
⇔−2x2−4x−2≤0⇔-2x2-4x-2≤0
⇔−2(x+1)2≤0⇔-2(x+1)2≤0 (##)
Ta có : ## đúng∀x∀x
⇒ # đúng ∀x∀x
⇒GTLN của A=3A=3 đạt khi x=−1


a) \(PT\Leftrightarrow x^2-4x+1=3x-5\)
\(\Leftrightarrow x^2-7x+6=0\Leftrightarrow\left(x-1\right)\left(x-6\right)=0\Leftrightarrow\orbr{\begin{cases}x=1\\x=6\end{cases}}\)
b) \(PT\Leftrightarrow x^2\left(2x-3\right)-\left(2x-3\right)=0\Leftrightarrow\left(x^2-1\right)\left(2x-3\right)=0\Leftrightarrow x\in\left\{\pm1;\frac{3}{2}\right\}\)

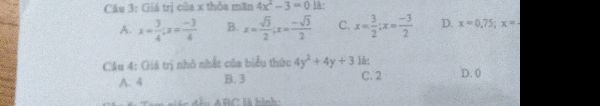
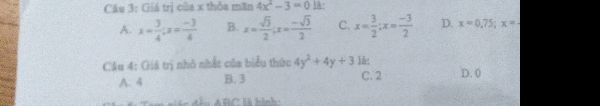
 mọi người giải giúp em bài này với ạ em đang cần gấp
mọi người giải giúp em bài này với ạ em đang cần gấp
a) \(\left(3x-4\right)^2=\left(3x\right)^2-2.3x.4+4^2=9x^2-24x+16\)
b) \(\left(x-2y\right)^2=x^2-4xy+4y^2\)
c) \(\left(3x-2\right)\left(3x+2\right)=9x^2-4\)
d) \(\left(3x+1\right)^2=9x^2+6x+1\)
e) \(\left(2x-3\right)^2=4x^2-12x+9\)
f) \(\left(3x-y\right)\left(9x^2+3xy+y^2\right)=27x^3-y^3\)