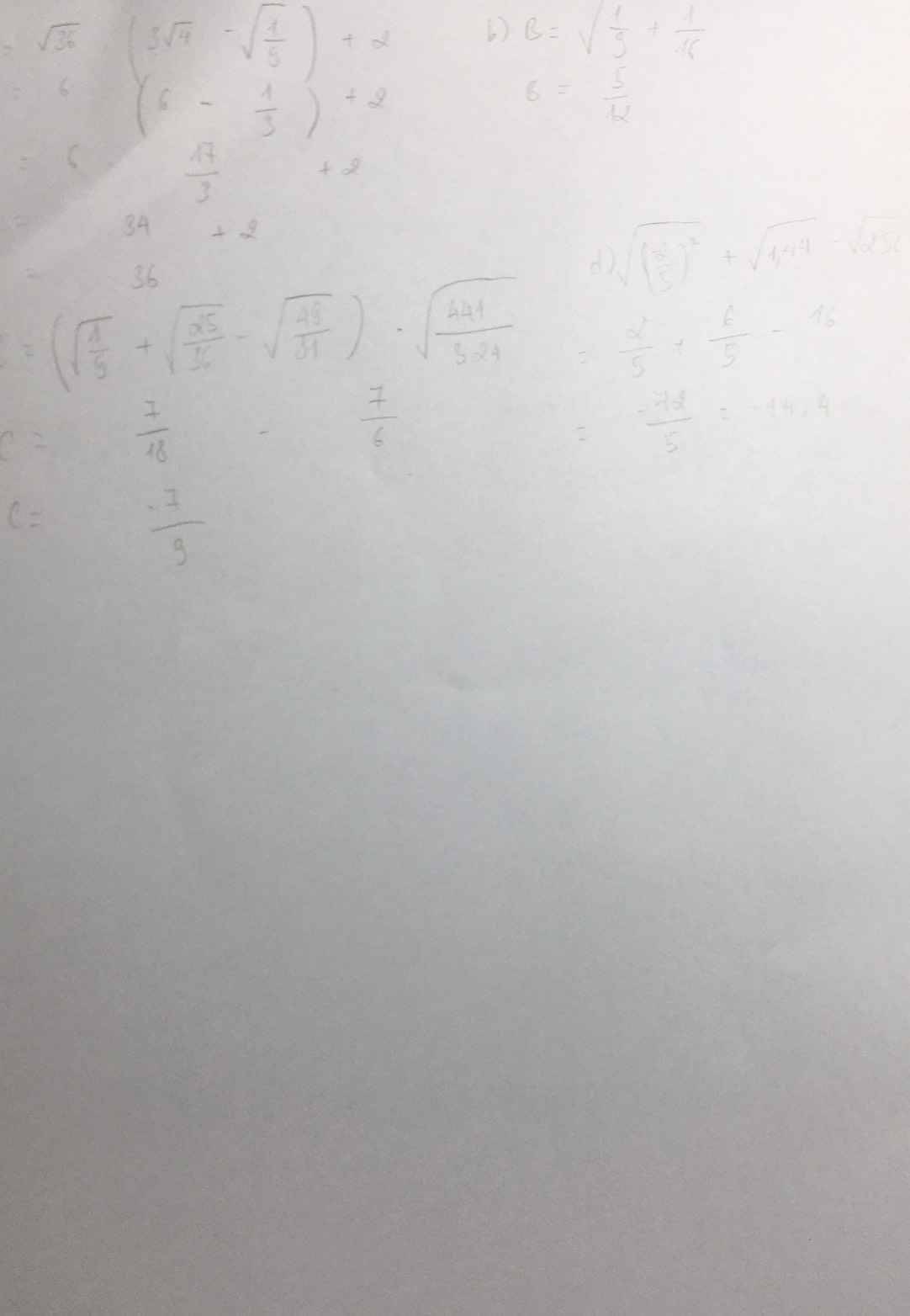a, đk x >= -2 

\(\left[{}\begin{matrix}2x+3=x+2\\2x+3=-x-2\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{5}{3}\end{matrix}\right.\left(tm\right)\)

b, đk x >= -7 

\(\left[{}\begin{matrix}5x-3=x+7\\5x-3=-x-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{11}{4}\\x=-\dfrac{2}{3}\end{matrix}\right.\left(tm\right)\)

a, |2x+3| = x + 2

đk x > -2

|2x + 3| = x + 2

với x > -3/2 ta có

2x+ 3 = x + 2 

2x - x = -3 + 2

x = -1

với  -2 < x < -3/2 ta có

-2x -3 = x + 2

 x + 2x = - 5

3x = -5

x = -5/3 (loại)

vậy x = -1

b, | 5x - 3|  - x = 7

|5x - 3| = 7 + x

đk x > -7

|5x - 3| =  7 + x

với x >3/5 

5x - 3 = 7 + x

5x - x = 7 + 3

4x = 10

x = 5/2 

với -7<x < 3/5 ta có

-5x + 3 = x + 7

x + 5x = 3 - 7

6x = -4

x = -2/3 

vậy x = -2/3 và x = 5/2 

đk x> =0 

\(\left|\sqrt{x}-1\right|=4\Leftrightarrow\left[{}\begin{matrix}\sqrt{x}-1=4\\\sqrt{x}-1=-4\end{matrix}\right.\Leftrightarrow x=25\)

| \(\sqrt{x}\) - 1| - 3 = 1 (đk x >0)

|\(\sqrt{x}\) - 1| = 1 + 3 

|\(\sqrt{x}\) - 1| = 4

\(\sqrt{x}\) - 1 =  +-4

\(\sqrt{x}\) =  5; \(\sqrt{x}\) = -3 (loại)

\(\sqrt{x}\) = 5 ⇔ x = 25

A = |x-y| + |x+1| + 2016

|x-y| ≥ 0 ; |x+1| ≥ 0 ⇔ |x-y| + |x+1| +2016 ≥ 2016

⇔ A(min)= 2016 ⇔ y= x = -1; 

\(A=\left|x-y\right|+\left|x+1\right|+2016\ge2016\)

Dấu ''='' xảy ra khi x = y = -1 

a, \(\left|x+6\right|+2\ge2\Rightarrow\dfrac{1}{\left|x+6\right|+2}\le\dfrac{1}{2}\)

Dấu ''='' xảy ra khi x = -6 

\(Q=-2\sqrt{x-3}+1\le1\)

Dấu ''='' xảy ra khi x = 3 

.

\(A=\sqrt{x}-1\ge-1\)

Dấu ''='' xảy ra khi x = 0 

Với x >= 0 ; x khác 4 

\(P=\dfrac{2\left(\sqrt{x}-2\right)+5}{\sqrt{x}-2}=2+\dfrac{5}{\sqrt{x}-2}\Rightarrow\sqrt{x}-2\inƯ\left(5\right)=\left\{\pm1;\pm5\right\}\)

\(P=\dfrac{2\sqrt{x}+1}{\sqrt{x}-2}=\dfrac{\left(2\sqrt{x}-4\right)+5}{\sqrt{x}-2}=\dfrac{2\sqrt{x}-4}{\sqrt{x}-2}+\dfrac{5}{\sqrt{x}-2}=2+\dfrac{5}{\sqrt{x}-2}\)

Để P đạt giá trị nguyên, \(\dfrac{5}{\sqrt{x}-2}\) phải đạt giá trị nguyên hay \(\sqrt{x}-2\in\left\{1,5,-1,-5\right\}\) 

\(\sqrt{x}-2=1\Rightarrow x=9\)

\(\sqrt{x}-2=5\Rightarrow x=49\)

\(\sqrt{x}-2=-1\Rightarrow x=1\)

\(\sqrt{x}-2=-5\Rightarrow\sqrt{x}=-3\left(vl\right)\)

Vậy \(x\in\left\{9,49,1\right\}\)

A = \(\sqrt{36}\).( 3\(\sqrt{4}\) - \(\sqrt{\dfrac{1}{9}}\)) + 2

A = 6( 3.2- \(\dfrac{1}{3}\)) + 2 

A = 6.3.2 - 2 + 2

A = 36

B = \(\sqrt{\dfrac{1}{9}+\dfrac{1}{16}}\)

B = \(\sqrt{\dfrac{25}{9.16}}\)

B = 5/12

C = ( \(\sqrt{\dfrac{1}{9}}\)+ \(\sqrt{\dfrac{25}{36}}\)- \(\sqrt{\dfrac{49}{81}}\)): \(\sqrt{\dfrac{441}{324}}\)

C = ( 1/3+ 5/6 - 7/9) : 7/6

C = ( 6/18 +15/18 -14/18): 7/6

C = 7/18 : 7/6

C = 7/18 .6/7

C = 1/3

D =\(\sqrt{(\dfrac{-2}{5})^2}\)+ \(\sqrt{1,44}\) - \(\sqrt{256}\)

D = 2/5 + 1,2 - 16

D = 0,4 + 1,2 - 16

D = -14,4