Cho hình vẽ:
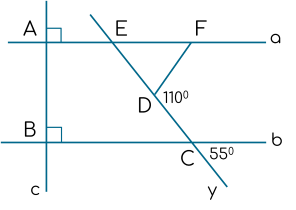
Biết $a \perp c$; $b \perp c$; $\widehat{FDC} = 110^{\circ}$ và $\widehat{bCy} = 55^{\circ}$.
a) Chứng minh $a$ // $b$.
b) Kẻ tia $Dn$ là tia phân giác của $\widehat{FDC}$. Chứng minh $Dn$ // $a$.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\Rightarrow\dfrac{x}{3}=\dfrac{y}{2}\)Theo tc dãy tỉ số bằng nhau ta có
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{10}{5}=2\Rightarrow x=6;y=4\)
Ta có : 2x = 3y => \(\dfrac{x}{3}=\dfrac{y}{2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\dfrac{x}{3}=\dfrac{y}{2}=\dfrac{x+y}{3+2}=\dfrac{10}{5}=2\) ( do x + y = 10 )
\(\Rightarrow\left\{{}\begin{matrix}x=2.3=6\\y=2.2=4\end{matrix}\right.\)

\(x-\dfrac{10}{3}=\dfrac{7}{15}.\dfrac{3}{5}\Leftrightarrow x-\dfrac{10}{3}=\dfrac{7}{25}\Leftrightarrow x=\dfrac{7}{25}+\dfrac{10}{3}=\dfrac{21+250}{75}=\dfrac{271}{75}\)

\(A=\dfrac{3x+6}{3x+1}=\dfrac{3x+1+5}{3x+1}=1+\dfrac{6}{3x+1}\)
\(\Rightarrow3x+1\inƯ\left(6\right)=\left\{\pm1;\pm2;\pm3;\pm6\right\}\)
| 3x+1 | 1 | -1 | 2 | -2 | 3 | -3 | 6 | -6 |
| x | 0 | loại | loại | -1 | loại | loại | loại | loại |
\(B=\dfrac{2x-8}{2x-1}=\dfrac{2x-7-1}{2x-1}=1-\dfrac{7}{2x-1}\Rightarrow2x-1\inƯ\left(-7\right)\left\{\pm1;\pm7\right\}\)
| 2x-1 | 1 | -1 | 7 | -7 |
| x | 1 | 0 | 4 | -3 |

Đổi 25%= 1/4
Lan ăn số táo là :
12 x 1/4 = 3 (quả)
Số táo còn lại là :
12-3 = 9 (quả )
Linh ăn số quả táo là :
9 x 1/3 =3 ( quả )
Lan ăn số quả táo là:
12 x 25 : 100 = 3 ( quả )
Còn lại số quả là:
12 - 3 = 9 ( quả )
Linh ăn số quả là:
9 x 1/3 = 3 ( quả)
Đáp số :...................

Đặt \(A=\dfrac{1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{99}}{\dfrac{1}{1.99}+\dfrac{1}{3.97}+...+\dfrac{1}{99.1}}\)
Đặt \(B=1+\dfrac{1}{3}+\dfrac{1}{5}+...+\dfrac{1}{99}\) ; \(C=\dfrac{1}{1.99}+\dfrac{1}{3.97}+...+\dfrac{1}{99.1}\)
=> \(A=\dfrac{B}{C}\) (*)
Ta có : \(C=\dfrac{1}{1.99}+\dfrac{1}{3.97}+...+\dfrac{1}{99.1}\)
\(\Rightarrow100C=\dfrac{100}{1.99}+\dfrac{100}{3.97}+...+\dfrac{100}{99.1}\)
\(\Rightarrow100C=\dfrac{99+1}{1.99}+\dfrac{97+3}{3.97}+...+\dfrac{99+1}{99.1}\)
\(\Rightarrow100C=1+\dfrac{1}{99}+\dfrac{1}{3}+\dfrac{1}{97}+...+\dfrac{1}{99}+1\)
\(\Rightarrow100C=2.\left(1+\dfrac{1}{3}+...+\dfrac{1}{99}\right)\)
\(\Rightarrow50C=1+\dfrac{1}{3}+...+\dfrac{1}{99}\)=B , kết hợp (*)
\(\Rightarrow A=\dfrac{B}{C}=\dfrac{50C}{C}=50\)
A B C D E F 1 2 2
Thầy ơi , đề sai ạ =))
a) Vì a ⊥ c ; b ⊥ c => a // b ( từ vuông góc đên song song )
b) Vì Dn là tia phân giác của \(\widehat{FDC}\) ( giả thiết )
\(\Rightarrow\widehat{D_1}=\widehat{D_2}=\dfrac{\widehat{FDC}}{2}=\dfrac{110^o}{2}=55^o\)
Mà \(\widehat{bCy}=55^o\) \(\Rightarrow\widehat{D_2}=\widehat{bCy}\) mà \(\widehat{D_2}\text{ và }\widehat{bCy}\) là 2 góc so le trong
=> Dn // b mà b // a ( phần a )
=> Dn // a