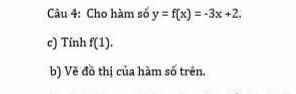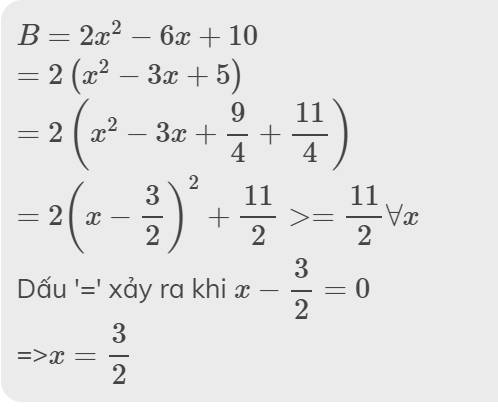Với a, b, c, d là các số thực phân biệt khác 0 và n là số nguyên thoả mãn (a^2-1)/5a= (b^2 −1) /5b = (c^2 −1)/ 3c = (d^2 −1)/3d = n. Chứng minh rằng (a−c)(b−c)(a+d)(b+d) là bình phương của một số nguyên
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Diện tích xung quanh hình chóp:
S = 4.10.13 : 2 = 260 (cm²)
b) Thể tích hình chóp:
V = 10 . 10 . 12 : 3 = 400 (cm³)

a) f(1) = -3.1 + 2 = -1
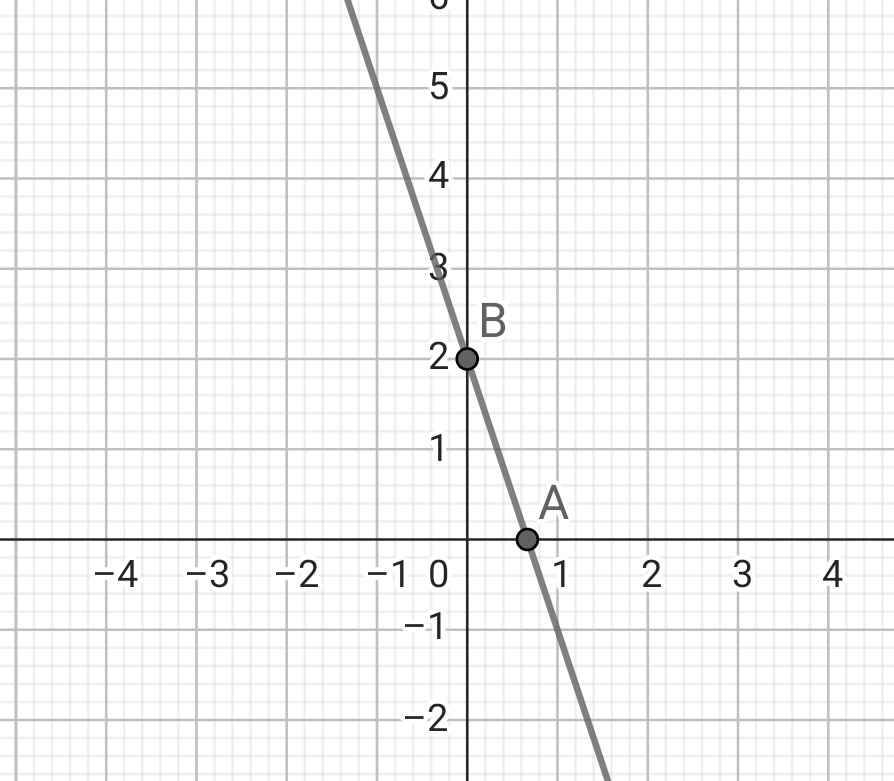
b) Cho x = 0 y = 2
Cho y = 0 x = 2/3
* Đồ thị:


Bạn xem lại phần số dính với biến là sao nhỉ?
Như $z^3\frac{7}{3}$ là sao ta?

Câu 4:
a: \(f\left(1\right)=-3\cdot1+2=-3+2=-1\)
b: 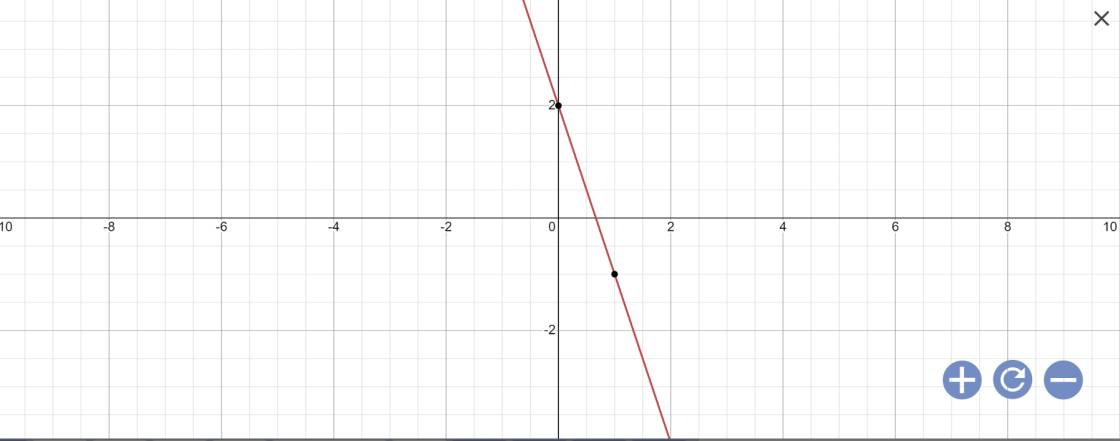
Câu 3:
a: \(f\left(1\right)=3\cdot1-2=3-2=1\)
b: 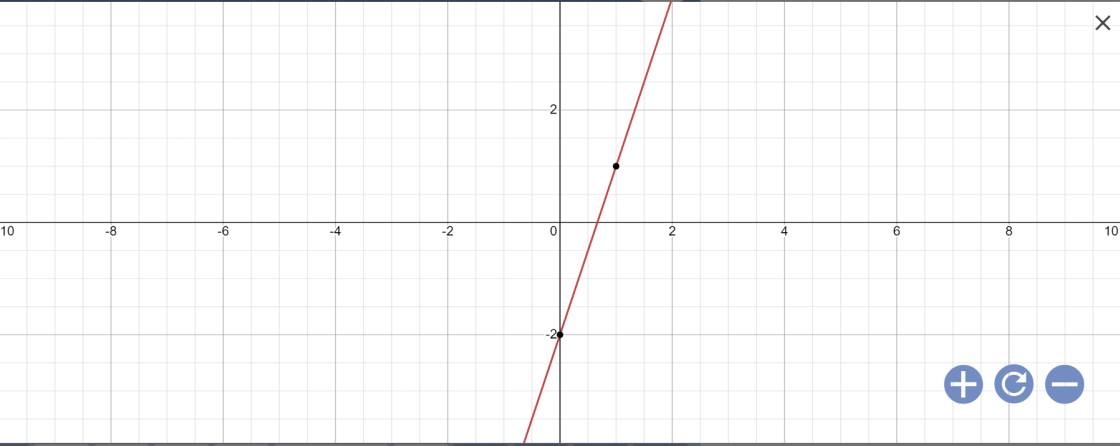
Câu 5:
Gọi độ dài quãng đường AB là x(km)
(ĐIều kiện: x>0)
Thời gian đi là \(\dfrac{x}{20}\left(giờ\right)\)
Thời gian về là \(\dfrac{x}{30}\left(giờ\right)\)
Thời gian về ít hơn thời gian đi là 15p=0,25 giờ nên ta có:
\(\dfrac{x}{20}-\dfrac{x}{30}=0,25\)
=>\(\dfrac{x}{60}=0,25\)
=>\(x=60\cdot0,25=15\left(nhận\right)\)
Vậy: Độ dài quãng đường AB là 15km

\(B=2x^2-6x+10\)
\(=2\left(x^2-3x+5\right)\)
\(=2\left(x^2-3x+\dfrac{9}{4}+\dfrac{11}{4}\right)\)
\(=2\left(x-\dfrac{3}{2}\right)^2+\dfrac{11}{2}>=\dfrac{11}{2}\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{3}{2}=0\)
=>\(x=\dfrac{3}{2}\)