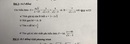
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\sqrt{2008}-\sqrt{2007}=\frac{\left(\sqrt{2008}-\sqrt{2007}\right)\cdot\left(\sqrt{2008}+\sqrt{2007}\right)}{\sqrt{2008}+\sqrt{2007}}=\frac{1}{\sqrt{2008}+\sqrt{2007}}\)
\(\sqrt{2010}-\sqrt{2009}=\frac{\left(\sqrt{2010}-\sqrt{2009}\right)\left(\sqrt{2010}+\sqrt{2009}\right)}{\sqrt{2010}+\sqrt{2009}}=\frac{1}{\sqrt{2010}+\sqrt{2009}}\)
\(\frac{1}{\sqrt{2008}+\sqrt{2007}}>\frac{1}{\sqrt{2010}+\sqrt{2009}}\)
Vậy \(\sqrt{2008}-\sqrt{2007}>\sqrt{2010}-\sqrt{2009}\)

\(\sqrt{3}< \sqrt{4}=2\)
\(5-\sqrt{8}=5-2\sqrt{2}\)
Mà :
\(2\sqrt{2}=\sqrt{8}< \sqrt{9}=3\)
Nên :
\(5-2\sqrt{2}>5-3=2\)
Vậy :
\(\sqrt{3}< 5-\sqrt{8}\)
√3<√4=23<4=2
5−√8=5−2√25−8=5−22 mà
2√2=√8<√9=322=8<9=3nFe=nFe2On=a(mol)nên 5−2√2>5−3=25−22>5−3=256a+a(112+16n)=14,4(1)
Vậy √3<5−√8nSO2=0,1(mol)
k cho mk nhé, cảm ơn

đk: \(x\ne-1\)
\(PT\Leftrightarrow x^2-\frac{2x^2}{x+1}+\left(\frac{x}{x+1}\right)^2+\frac{2x^2}{x+1}=1\)
\(\Leftrightarrow\left(x-\frac{x}{x+1}\right)^2+2\frac{x^2}{x+1}=1\)
\(\Leftrightarrow\left(\frac{x^2}{x+1}+1\right)^2=2\)
\(\Leftrightarrow\orbr{\begin{cases}x^2+\left(1-\sqrt{2}\right)x+\left(1-\sqrt{2}\right)=0\\x^2+\left(1+\sqrt{2}\right)x+\left(1+\sqrt{2}\right)=0\end{cases}}\)
\(\Leftrightarrow\orbr{\begin{cases}\frac{\sqrt{2}-1+\sqrt{2\sqrt{2}-1}}{2}\\\frac{\sqrt{2}-1-\sqrt{2\sqrt{2}-1}}{2}\end{cases}\left(TM\right)}\)
Theo hđt : \(\left(a-b\right)^2=a^2-2ab+b^2\Rightarrow a^2+b^2=\left(a-b\right)^2+2ab\)
pt có dạng : \(\left(x-\frac{x}{x+1}\right)^2+\frac{2x^2}{x+1}=1\)ĐK : \(x\ne1\)
\(\Leftrightarrow\left(\frac{x^2+x-x}{x+1}\right)^2+\frac{2x^2}{x+1}=1\Leftrightarrow\frac{x^4+2x^2}{x+1}=\frac{x+1}{x+1}\)
\(\Rightarrow x^4+2x^2-x-1=0\Rightarrow x_1=-0,48...;x_2=0,82...\)( tmđk )

\(\frac{-19\sqrt{6-46}}{5}\approx-18.508061\)
Chúc anh học tốt!






Bài 3 :
a, \(x=3-2\sqrt{2}\Rightarrow\sqrt{x}=\sqrt{3-2\sqrt{2}}=\sqrt{2}-1\)
Thay vào B ta được : \(B=\frac{7}{\sqrt{2}-1+3}=\frac{7}{\sqrt{2}+2}=\frac{7}{\sqrt{2}+2}\)
\(=\frac{7\left(\sqrt{2}-2\right)}{2-4}=-\frac{7\sqrt{2}-14}{2}\)
b, Với \(x\ge0;x\ne25\)
\(A=\frac{6\sqrt{x}}{x-25}-\frac{3}{\sqrt{x}+5}+\frac{4}{\sqrt{x}-5}\)
\(=\frac{6\sqrt{x}-3\left(\sqrt{x}-5\right)+4\left(\sqrt{x}+5\right)}{x-25}\)
\(=\frac{3\sqrt{x}+15+4\sqrt{x}+20}{x-25}=\frac{7\sqrt{x}+35}{x-25}=\frac{7}{\sqrt{x}-5}\)
Ta có : \(M=\frac{A}{B}=\frac{7}{\sqrt{x}-5}.\frac{\sqrt{x}+3}{7}=\frac{\sqrt{x}+3}{\sqrt{x}-5}\)
c, \(M< \frac{1}{2}\Rightarrow\frac{\sqrt{x}+3}{\sqrt{x}-5}-\frac{1}{2}< 0\)
\(\Leftrightarrow\frac{2\sqrt{x}+6-\sqrt{x}+5}{2\sqrt{x}-10}< 0\Leftrightarrow\frac{\sqrt{x}+11}{2\sqrt{x}-10}< 0\)
\(\Rightarrow\sqrt{x}-5< 0\Leftrightarrow x< 25\)
Kết hợp với đk vậy 0 =< x < 25