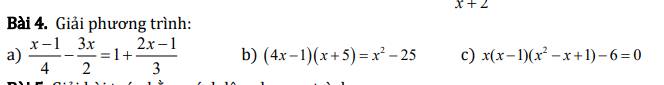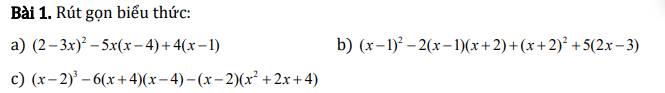Cho △ABC cân tại A, 2 đường cao AI và BH cắt nhau tại H. Gọi E là giao điểm của CH và AB, T là giao điểm của DE và AH. Chứng minh: EH, EA lần lượt là phân giác trong và phân giác ngoài của △ETI tại đỉnh E
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
$a^2+b^2<2$
$\Leftrightarrow (a-b)^2+2ab<2$
$\Leftrightarrow ab< \frac{2-(a-b)^2}{2}\leq \frac{2}{2}=1$
BĐT cần chứng minh tương đương với:
$\frac{a^2+b^2+2}{(a^2+1)(b^2+1)}\leq \frac{2}{1+ab}$
$\Leftrightarrow (a^2+b^2+2)(1+ab)\leq 2(a^2+1)(b^2+1)$
$\Leftrightarrow a^2+b^2+2+ab(a^2+b^2+2)\leq 2(a^2b^2+a^2+b^2+1)$
$\Leftrightarrow ab(a^2+b^2+2)\leq 2a^2b^2+a^2+b^2$
$\Leftrightarrow ab(a^2+b^2-2ab)-(a^2+b^2-2ab)\leq 0$
$\Leftrightarrow ab(a-b)^2-(a-b)^2\leq 0$
$\Leftrightarrow (a-b)^2(ab-1)\leq 0$ (luôn đúng với mọi $a,b\in\mathbb{R}$ và $ab<1$)
Do đó ta có đpcm.

a: Xét ΔBHE vuông tại E và ΔCHF vuông tại F có
\(\widehat{BHE}=\widehat{CHF}\)(hai góc đối đỉnh)
Do đó; ΔBHE~ΔCHF
b: Xét ΔAEH vuông tại E và ΔADB vuông tại D có
\(\widehat{EAH}\) chung
Do đó: ΔAEH~ΔADB
=>\(\dfrac{AE}{AD}=\dfrac{AH}{AB}\)
=>\(AE\cdot AB=AH\cdot AD\)
c: Xét ΔAFB vuông tại F và ΔAEC vuông tại E có
\(\widehat{FAB}\) chung
Do đó: ΔAFB~ΔAEC
=>\(\dfrac{AF}{AE}=\dfrac{AB}{AC}\)
=>\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
Xét ΔAFE và ΔABC có
\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
Do đó: ΔAFE~ΔABC
=>\(\dfrac{AF}{AB}=\dfrac{AE}{AC}\)
\(\left(\dfrac{AF}{AB}\right)^2=\dfrac{1}{2}\)
=>\(\dfrac{AF}{AB}=\dfrac{\sqrt{2}}{2}=\dfrac{AE}{AC}\)
Xét ΔAEC vuông tại E có \(sinACE=\dfrac{AE}{AC}=\dfrac{\sqrt{2}}{2}\)
nên \(\widehat{ACE}=45^0\)
=>\(\widehat{ABF}=45^0\)
Xét tứ giác BEHD có \(\widehat{BEH}+\widehat{BDH}=90^0+90^0=180^0\)
nên BEHD là tứ giác nội tiếp
=>\(\widehat{EDH}=\widehat{EBH}=45^0\)
Xét tứ giác DCFH có \(\widehat{HDC}+\widehat{HFC}=90^0+90^0=180^0\)
nên DCFH là tứ giác nội tiếp
=>\(\widehat{HDF}=\widehat{HCF}=45^0\)
\(\widehat{EDF}=\widehat{EDH}+\widehat{FDH}=45^0+45^0=90^0\)
=>ΔEDF vuông tại D

a: \(\dfrac{x-1}{4}-\dfrac{3x}{2}=1+\dfrac{2x-1}{3}\)
=>\(\dfrac{x-1-6x}{4}=\dfrac{3+2x-1}{3}\)
=>\(\dfrac{-5x-1}{4}=\dfrac{2x+2}{3}\)
=>\(4\left(2x+2\right)=3\left(-5x-1\right)\)
=>-15x-3=8x+8
=>-23x=11
=>\(x=-\dfrac{11}{23}\)
b: \(\left(4x-1\right)\left(x+5\right)=x^2-25\)
=>\(\left(4x-1\right)\left(x+5\right)-\left(x-5\right)\left(x+5\right)=0\)
=>\(\left(x+5\right)\left(4x-1-x+5\right)=0\)
=>(x+5)(3x+4)=0
=>\(\left[{}\begin{matrix}x=-5\\x=-\dfrac{4}{3}\end{matrix}\right.\)
c: \(x\left(x-1\right)\left(x^2-x+1\right)-6=0\)
=>\(\left(x^2-x\right)\left(x^2-x+1\right)-6=0\)
=>\(\left(x^2-x\right)^2+\left(x^2-x\right)-6=0\)
=>\(\left(x^2-x+3\right)\left(x^2-x-2\right)=0\)
mà \(x^2-x+3=\left(x-\dfrac{1}{2}\right)^2+\dfrac{11}{4}>0\forall x\)
nên \(x^2-x-2=0\)
=>(x-2)(x+1)=0
=>\(\left[{}\begin{matrix}x=2\\x=-1\end{matrix}\right.\)

a: Thay x=5 vào A, ta được:
\(A=\dfrac{5+3}{5^2}=\dfrac{8}{25}\)
b: \(B=\dfrac{x-6}{x^2-4}+\dfrac{3}{x-2}+\dfrac{x}{x+2}\)
\(=\dfrac{x-6}{\left(x-2\right)\left(x+2\right)}+\dfrac{3}{x-2}+\dfrac{x}{x+2}\)
\(=\dfrac{x-6+3\left(x+2\right)+x\left(x-2\right)}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x-6+3x+6+x^2-2x}{\left(x-2\right)\left(x+2\right)}\)
\(=\dfrac{x^2+2x}{\left(x-2\right)\left(x+2\right)}=\dfrac{x}{x-2}\)
c: \(P=A\cdot B=\dfrac{x}{x-2}\cdot\dfrac{x+3}{x^2}=\dfrac{x+3}{x\left(x-2\right)}\)
\(P=\dfrac{1}{x+2}\)
=>\(\dfrac{x+3}{x\left(x-2\right)}=\dfrac{1}{x+2}\)
=>\(x\left(x-2\right)=\left(x+3\right)\left(x+2\right)\)
=>\(x^2+5x+6=x^2-2x\)
=>7x=-6
=>\(x=-\dfrac{6}{7}\left(nhận\right)\)

a: \(3x\left(x-7\right)+2xy-14y\)
\(=3x\left(x-7\right)+2y\left(x-7\right)\)
=(x-7)(3x+2y)
b: \(\left(4x-y\right)\left(a+b\right)-\left(y-4x\right)\left(b-1\right)\)
\(=\left(4x-y\right)\left(a+b\right)+\left(4x-y\right)\left(b-1\right)\)
\(=\left(4x-y\right)\left(a+b+b-1\right)\)
\(=\left(4x-y\right)\left(a+2b-1\right)\)
c: \(2x^2-x-6xy+3y\)
\(=\left(2x^2-x\right)-\left(6xy-3y\right)\)
\(=x\left(2x-1\right)-3y\left(2x-1\right)\)
\(=\left(2x-1\right)\left(x-3y\right)\)
d: \(x^2-z^2+4xy+4y^2\)
\(=\left(x^2+4xy+4y^2\right)-z^2\)
\(=\left(x+2y\right)^2-z^2\)
\(=\left(x+2y+z\right)\left(x+2y-z\right)\)

a: \(\left(2-3x\right)^2-5x\left(x-4\right)+4\left(x-1\right)\)
\(=9x^2-12x+4-5x^2+20x+4x-4\)
\(=4x^2+12x\)
b: \(\left(x-1\right)^2-2\left(x-1\right)\left(x+2\right)+\left(x+2\right)^2+5\left(2x-3\right)\)
\(=x^2-2x+1-2\left(x^2+x-2\right)+x^2+4x+4+10x-15\)
\(=2x^2+12x-14-2x^2-2x+4\)
=10x-10
c: \(\left(x-2\right)^3-6\left(x+4\right)\left(x-4\right)-\left(x-2\right)\left(x^2+2x+4\right)\)
\(=x^3-6x^2+12x-8-\left(x^3-8\right)-6\left(x^2-16\right)\)
\(=x^3-6x^2+12x-8-x^3+8-6x^2+96\)
\(=-12x^2+12x+96\)

a: Xét ΔABC có
D,E lần lượt là trung điểm của AB,AC
=>DE là đường trung bình của ΔABC
=>DE//BC và BC=2DE
b: Xét ΔAFB có
D là trung điểm của AB
DI//FB
Do đó: I là trung điểm của AF
Xét ΔAFB có ID//FB
nên \(\dfrac{ID}{FB}=\dfrac{AD}{AB}=\dfrac{1}{2}\)
Xét ΔAFC có IE//FC
nên \(\dfrac{IE}{FC}=\dfrac{AE}{AC}=\dfrac{1}{2}\)
Do đó: \(\dfrac{ID}{FB}=\dfrac{IE}{FC}\)
mà ID=IE(I là trung điểm của DE)
nên FB=FC
=>F là trung điểm của BC
Xét tứ giác AEFD có
I là trung điểm chung của AF và ED
=>AEFD là hình bình hành
Hình bình hành AEFD có \(\widehat{EAD}=90^0\)
nên AEFD là hình chữ nhật
c: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(DE=\dfrac{1}{2}BC=\dfrac{1}{2}\cdot10=5\left(cm\right)\)
I là trung điêm của DE
=>ID=IE=DE/2=2,5(cm)
=>AI=ED/2=2,5(cm)
ΔABC vuông tại A
mà AF là đường trung tuyến
nên AF=BC/2=5(cm)
Xét ΔABC có
BE,AF là các đường trung tuyến
BE cắt AF tại K
Do đó: K là trọng tâm của ΔABC
=>\(AK=\dfrac{2}{3}AF=\dfrac{2}{3}\cdot5=\dfrac{10}{3}\left(cm\right)\)
AI+IK=AK
=>\(IK+2,5=\dfrac{10}{3}\)
=>\(IK=\dfrac{10}{3}-\dfrac{5}{2}=\dfrac{20}{6}-\dfrac{15}{6}=\dfrac{5}{6}\left(cm\right)\)