(1+1/100)x(1+1/101)x(1+1/102)x...x(1+2012)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC=\sqrt{5^2-3^2}=4\left(cm\right)\)
Xét ΔABC vuông tại A có \(tanC=\dfrac{AB}{AC}=\dfrac{3}{4}\)
nên \(\widehat{C}\simeq37^0\)
ΔABC vuông tại A
=>\(\widehat{ABC}+\widehat{ACB}=90^0\)
=>\(\widehat{ABC}=90^0-37^0=53^0\)
b: Xét ΔBDC vuông tại B có BA là đường cao
nên \(BA^2=AD\cdot AC\)
=>\(AD=\dfrac{3^2}{4}=\dfrac{9}{4}=2,25\left(cm\right)\)
ΔABD vuông tại A
=>\(AB^2+AD^2=BD^2\)
=>\(BD=\sqrt{2,25^2+3^2}=3,75\left(cm\right)\)
Xét ΔBAD vuông tại A có AF là đường cao
nên \(BF\cdot BD=BA^2\left(1\right)\)
Xét ΔBAC vuông tại A có AE là đường cao
nên \(BE\cdot BC=BA^2\left(2\right)\)
Từ (1),(2) suy ra \(BF\cdot BD=BE\cdot BC\)
Xét tứ giác AEBF có \(\widehat{AEB}=\widehat{AFB}=\widehat{EBF}=90^0\)
nên AEBF là hình chữ nhật
ΔABC vuông tại A có AE là đường cao
nên \(\left\{{}\begin{matrix}AE\cdot BC=AB\cdot AC\\BE\cdot BC=BA^2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AE=\dfrac{3\cdot4}{5}=2,4\left(cm\right)\\BE=\dfrac{3^2}{5}=1,8\left(cm\right)\end{matrix}\right.\)
AEBF là hình chữ nhật
=>\(S_{AEBF}=AE\cdot BE=2,4\cdot1,8=4,32\left(cm^2\right)\)

Ta có:
1.2.3.4.5.6 + 6390
= 10.3.4 + 639.10
= 10.(3.4 + 639)
= 2.5.(3.4 + 3.213)
= 2.5.[3(4 + 213)]
⇒ (1.2.3.4.5.6 + 6390) chia hết cho 2; 3; 5.
Nhưng 4 + 213 = 217 không chia hết cho 9
⇒ (1.2.3.4.5.6 + 6390) không chia hết cho 9.
pencil sai
1.2.3.4.5.6 + 6390
= 2 . 3.2.2.5.2.3 + 10 . 639
= 10 . 8. 9 + 10 . 9 . 71
= 10 . 9 . ( 8 + 71)
= 2 . 5 . 9 . 79
2 chia hết cho 2
5 chia hết cho 5
9 chia hết cho 3 và 9
vậy suy ra tổng (1.2.3.4.5.6 + 6390 ) có chia hết cho 4 số 2 ; 3;5;9

\(10^{28}⋮8;8⋮8\)
Do đó: \(10^{28}+8⋮8\)
\(10^{28}+8=10...08\)
Tổng các chữ số là 1+0+...+0+8=18\(⋮9\)
=>\(10^{28}+8⋮9\)
mà \(10^{28}+8⋮8\)
mà ƯCLN(9;8)=1
nên \(10^{28}+8⋮9\cdot8=72\)

\(\dfrac{7}{12}:\dfrac{7}{9}=\dfrac{7}{12}\times\dfrac{9}{7}=\dfrac{9}{12}=\dfrac{3}{4}\)

\(\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+...+\dfrac{1}{2007\times2009}+\dfrac{1}{2009\times2011}\\ =\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{2007\times2009}+\dfrac{2}{2009\times2011}\right)\\ =\dfrac{1}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...-\dfrac{1}{2009}+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\\ =\dfrac{1}{2}\times\left(1-\dfrac{1}{2011}\right)\\ =\dfrac{1}{2}\times\dfrac{2010}{2011}\\ =\dfrac{1005}{2011}\)

Độ dài đường chéo thứ nhất là:
411:3x2=274(m)
Độ dài đường chéo thứ hai là:
274:2=137(m)
Diện tích hình thoi là: \(274\cdot\dfrac{137}{2}=18769\left(m^2\right)\)
Tỉ số đường chéo thứ nhất và đường chéo thứ hai là: \(\dfrac{2}{1}\)
Tổng số phần bằng nhau là:
\(2+1=3\) (phần)
Đường chéo thứ nhất là:
\(411:3\cdot2=274\left(m\right)\)
Đường chéo thứ hai là:
\(411-274=137\left(m\right)\)
Diện tích hình thoi là:
\(\dfrac{274\cdot137}{2}=18769\left(m^2\right)\)
Đáp số: \(18769m^2\)

Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)
=5145484985742651291274572147214912742724765142721567
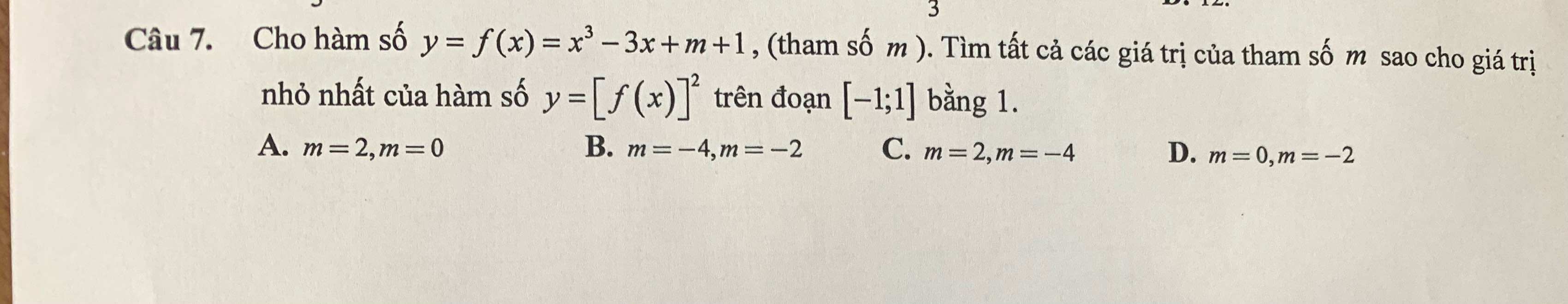
\(\left(1+\dfrac{1}{100}\right)\times\left(1+\dfrac{1}{101}\right)\times\left(1+\dfrac{1}{102}\right)\times...\times\left(1+\dfrac{1}{2012}\right)\)
\(=\dfrac{101}{100}\times\dfrac{102}{101}\times\dfrac{103}{102}\times...\times\dfrac{2013}{2012}\)
\(=\dfrac{101\times102\times103\times...\times2013}{100\times101\times102\times...\times2012}\)
\(=\dfrac{2013}{100}\)