$(2x+1)^3=(2x+1)^4$
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


x2(x-7)<0
xét x2(x-7) = 0
⇔ x=0; x = 7
lập bảng xét dấu ta có (có bảng xét dấu kèm theo )
0 # x < 7
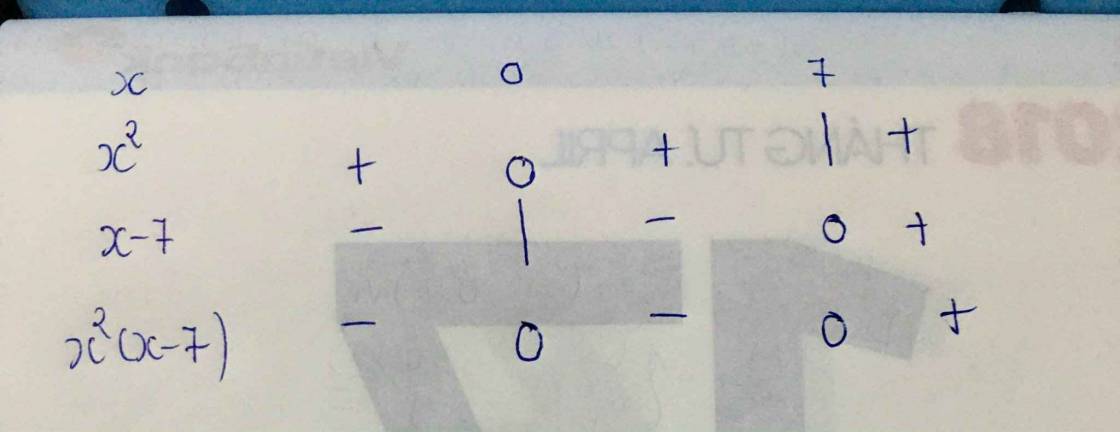

A (đúng):vì mọi số hữu tỉ âm luôn nhỏ hơn số hữu tỉ dương.
B (sai): vì 0 không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm.
C (sai): vì tập hợp số nguyên âm là số hữu tỉ âm
D (sai):vì tập hợp Q gồm các số hữu tỉ dương, các số hữu tỉ âm và số 0
Đáp án là: A

câu 1: (mik lm lun nha ko chép lại đề đou)
lx+1/2l = 7/3 - (-1/4)
lx+1/2l= 31/12
x+1/2 = 31/12 hoặc x+1/2= -31/12
x=31/12 - 1/2 x=-31/12 -1/2
x= 25/12 x= -37/12
Vậy x thuộc { 25/12 ; 37/12}
Câu 2 :mik chịu nuôn =((

a, Tam giác ABC vuông tại A có
Góc BCA+ góc ABC= 1800
Mà gócABC= 600 nên góc C=300
b, AD là tia p/g của góc A nên
Góc BAD=45 độ
Áp dụng định lí tổng 3 góc (.) 1 tg vào tg BAD có. Góc A+B+D=180 độ
Do đó góc ADH=75 độ
c, ADC là góc ngoài Th nên ADC=90+HAD
Mà ADC=105 độ nên HAD=15 độ

a) \(\dfrac{x}{2,4}=\dfrac{y}{-6,5}\Leftrightarrow-6,5x=2,4y\left(1\right)\)
\(y-x=-8,9\Leftrightarrow y=-8,9+x\left(2\right)\)
Thế (2) vào (1) ta có:
\(-6,5x=2,4\left(-8,9+x\right)\)
\(-6,5x-2,4x=2,4.\left(-8,9\right)\)
\(-8,9x=-21,36\)
\(x=2,4\)
\(\Rightarrow y=-6,5\)
b) \(\dfrac{x}{y}=\dfrac{5}{9}\Leftrightarrow5y=9x\left(1\right)\)
\(x+y=70\Rightarrow x=70-y\left(2\right)\)
Thế (2) vào (1) ta có:
\(5y=9\left(70-y\right)\)
\(5y+9y=70\)
\(14y=70\Rightarrow y=5\)
\(\Rightarrow x=65\)

a, Thể tích bể nước là: 2 x 1,2 x 0,8 = 1,92 ( lít )

Bạn tự vẽ hình nhé !
a)\widehat{BAD}< \widehat{BMD}BAD<BMD(vì\widehat{BMD}BMDlà góc ngoài của\Delta ABMΔABM)(1)
b)\widehat{CAD}< \widehat{CMD}CAD<CMD(vì\widehat{CMD}CMDlà góc ngoài của\Delta CAMΔCAM)(2)
Từ (1) và (2) :\widehat{BAD}+\widehat{CAD}< \widehat{BMD}+\widehat{CMD}\Leftrightarrow\widehat{BAC}< \widehat{BMC}BAD+CAD<BMD+CMD⇔BAC<BMC

\((x-\dfrac{1}{2})^2-\dfrac{1}{2}=\dfrac{23}{12}\)
\((x-\dfrac{1}{2})^2=\dfrac{23}{12}+\dfrac{1}{2}\)
\((x-\dfrac{1}{2})^2=\dfrac{29}{12}\)
\(\left[{}\begin{matrix}x-\dfrac{1}{2}=\sqrt{\dfrac{29}{12}}\\x-\dfrac{1}{2}=-\sqrt{\dfrac{29}{12}}\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=\sqrt{\dfrac{29}{12}}+\dfrac{1}{2}\\x=-\sqrt{\dfrac{29}{12}}+\dfrac{1}{2}\end{matrix}\right.\)
(2x +1)3 = (2x +1)4
(2x + 1)4 - (2x + 1 )3 =0
(2x + 1)3(2x +1-1) =0
2x(2x+1)3= 0
\(\left[{}\begin{matrix}x=0\\2x+1=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{2}\end{matrix}\right.\)