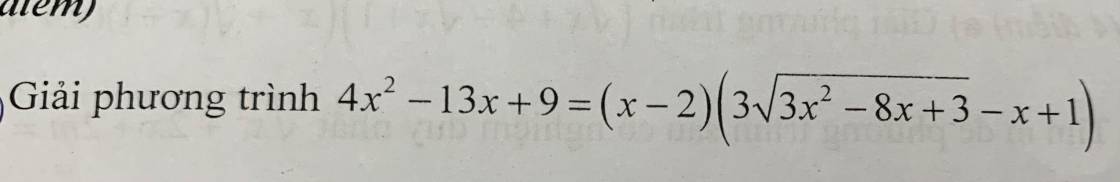Mọi người giúp mình với ạ. Mình cảm ơn!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


NB
1

AH
Akai Haruma
Giáo viên
2 tháng 3 2024
Lời giải:
PT $\Leftrightarrow 5x^2-16x+11=3(x-2)\sqrt{3x^2-8x+3}$
Đặt $x-2=a; \sqrt{3x^2-8x+3}=b(b\geq 0)$
Khi đó:
$2a^2+b^2=2(x-2)^2+(3x^2-8x+3)=5x^2-16x+11$
PT đã cho trở thành:
$2a^2+b^2=3ab$
$\Leftrightarrow 2a^2+b^2-3ab=0$
$\Leftrightarrow (a-b)(2a-b)=0$
$\Leftrightarrow a=b$ hoặc $2a=b$
Nếu $a=b$
$\Leftrightarrow x-2=\sqrt{3x^2-8x+3}$
$\Leftrightarrow (x-2)^2=3x^2-8x+3$ ($x\geq 2$)
$\Leftrightarrow 2x^2-4x-1=0$
$\Leftrightarrow x=\frac{2\pm \sqrt{6}}{2}$
Do $x\geq 2$ nên $x=\frac{2+\sqrt{6}}{2}$
Nếu $2a=b$
$\Leftrightarrow 2(x-2)=\sqrt{3x^2-8x+3}$
$\Leftrightarrow 4(x-2)^2=3x^2-8x+3$ ($x\geq 2$)
$\Leftrightarrow x^2-8x+13=0$
$\Leftrightarrow x=4\pm \sqrt{3}$