1/1x3+1/3x5+1/5x7+...+1/2007x2009+1/2009x2011
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Độ dài đường chéo thứ nhất là:
411:3x2=274(m)
Độ dài đường chéo thứ hai là:
274:2=137(m)
Diện tích hình thoi là: \(274\cdot\dfrac{137}{2}=18769\left(m^2\right)\)
Tỉ số đường chéo thứ nhất và đường chéo thứ hai là: \(\dfrac{2}{1}\)
Tổng số phần bằng nhau là:
\(2+1=3\) (phần)
Đường chéo thứ nhất là:
\(411:3\cdot2=274\left(m\right)\)
Đường chéo thứ hai là:
\(411-274=137\left(m\right)\)
Diện tích hình thoi là:
\(\dfrac{274\cdot137}{2}=18769\left(m^2\right)\)
Đáp số: \(18769m^2\)

Nếu \(f\left(x\right)=0\) có nghiệm trên \(\left[-1;1\right]\Rightarrow\min\limits_{\left[-1;1\right]}\left[f\left(x\right)\right]^2=0\) ko thỏa mãn yêu cầu
\(\Rightarrow f\left(x\right)=0\) vô nghiệm trên \(\left[-1;1\right]\)
Khi đó
\(f'\left(x\right)=3x^2-3=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)
\(\Rightarrow f'\left(x\right)\le0;\forall x\in\left[-1;1\right]\)
Xét hàm \(y=\left[f\left(x\right)\right]^2\) trên \(\left[-1;1\right]\)
\(y=\left[f\left(x\right)\right]^2\Rightarrow y'=2f'\left(x\right).f\left(x\right)\)
Do \(f'\left(x\right)\le0\) và \(f\left(x\right)=0\) vô nghiệm (nên ko đổi dấu) trên \(\left[-1;1\right]\) nên:
TH1: \(f\left(x\right)>0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1>-m\)
\(\Rightarrow-m< \min\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=-1\)
\(\Rightarrow m>1\)
Khi đó \(f'\left(x\right).f\left(x\right)\le0\Rightarrow y=\left[f\left(x\right)\right]^2\) nghịch biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(1\right)=\left(1-3+m+1\right)^2=\left(m-1\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=0< 1\left(loại\right)\\m=2\end{matrix}\right.\)
TH2: \(f\left(x\right)< 0;\forall x\in\left[-1;1\right]\Rightarrow x^3-3x+1< -m\)
\(\Rightarrow-m>\max\limits_{\left[-1;1\right]}\left(x^3-3x+1\right)=3\)
\(\Rightarrow m< -3\)
Khi đó \(f'\left(x\right).f\left(x\right)\ge0\Rightarrow y=\left[f\left(x\right)\right]^2\) đồng biến trên \(\left[-1;1\right]\)
\(\Rightarrow y_{min}=y\left(-1\right)=\left(-1+3+m+1\right)^2=\left(m+3\right)^2=1\)
\(\Rightarrow\left[{}\begin{matrix}m=-2>-3\left(loại\right)\\m=-4\end{matrix}\right.\)
Vậy \(m=2;m=-4\) (C đúng)
=5145484985742651291274572147214912742724765142721567
\(\text{Viết các số 9673,3547:}\)\(\overline{abcde}\)\(\text{ dưới dạng tổng các luỹ thừa của 10.}\)

`9673=9000+600+70+3`
`=9*10^3+6*10^2+7*10+3`
`3547=3000+500+40+7`
`=3*10^3+5*10^2+4*10+7`
\(\overline{abcde}\)`=a*10000+b*1000+c*100+d*10+e`
`=a*10^4+b*10^3+c*10^2+d*10+e`
\(9673=9\cdot10^3+6\cdot10^2+7\cdot10^1+3\cdot10^0\\ 3547=3\cdot10^3+5\cdot10^2+4\cdot10^1+7\cdot10^0\\ abcde=a\cdot10^4+b\cdot10^3+c\cdot10^2+d\cdot10^1+e\cdot10^0\)

\(\dfrac{2}{5\times7}+\dfrac{2}{7\times9}+...+\dfrac{2}{13\times15}\)
\(=\dfrac{1}{5}-\dfrac{1}{7}+\dfrac{1}{7}-\dfrac{1}{9}+...+\dfrac{1}{13}-\dfrac{1}{15}\)
\(=\dfrac{1}{5}-\dfrac{1}{15}=\dfrac{2}{15}\)
`2/(5 xx 7)+2/(7 xx 9) + ... + 2/(13 xx 15)`
`=1/5-1/7+1/7-1/9+...+1/13-1/15`
`=1/5+(1/7-1/7)+(1/9-1/9)+...+(1/13-1/13)-1/15`
`=1/5-1/15`
`=3/15-1/15`
`=2/15`

1 She uses it
2 She has lost it
3 We got them
4 She enjoys
5 I hate it
6 I have checked them
7 They play it
8 You have not watered them
1. Sarah finds her mobile phone very useful. She uses it all the time.
2. Vicky doesn't know where her watch is. She has lost it.
3. We're in the middle of decorating our kitchen, so we can't cook any meals. We're getting them from a take-away restaurant this week.
4. Claire is on a skiing holiday. She is enjoying it, she says on her postcard.
5. The colour of this paint is absolutely awful. I hate it.
6. These figures certainly should add up. I have checked them several times already.
7. Trevor and Laura like Scrabble. They play it most evenings.
8. These flowers are dying. You haven't watered them for ages.

Ta có:
\(25^9=\left(5^2\right)^9=5^{18}\)
Vì: \(5^{17}< 5^{18}\) nên \(5^{17}< 25^9\)
Ta có:
\(3^{90}=\left(3^3\right)^{30}=27^{30}\)
\(4^{60}=\left(4^2\right)^{30}=16^{30}\)
Vì: \(27^{30}>16^{30}\) nên \(3^{90}>4^{60}\)
Bài 1:
c: \(18\cdot\left[\left(3^4\cdot29+3^4\cdot6+3^4\cdot34\right)-71\cdot1^{56}\right]-80\)
\(=18\cdot\left[3^4\left(29+6+34\right)-71\right]-80\)
\(=18\cdot\left[81\cdot69-71\right]-80\)
\(=18\cdot5518-80=99244\)
b: \(\left[19+\left(3^5-62\right)\right]\cdot x=10^3\cdot10\)
=>\(\left(243-62+19\right)\cdot x=10000\)
=>\(200x=10000\)
=>x=10000:200=50
Bài 2:
\(25^9=\left(5^2\right)^9=5^{18}>5^{17}\)
\(3^{90}=\left(3^3\right)^{30}=27^{30};4^{60}=\left(4^2\right)^{30}=16^{30}\)
mà 27>16
nên \(3^{90}>4^{60}\)

Chiều cao của hình bình hành là:
\(189:7=27\left(m\right)\)
Diện tích ban đầu là \(47\cdot\dfrac{27}{2}=634,5\left(m^2\right)\)
Sau khi mở rộng, cạnh đáy mới là:
\(47+7=54\left(m\right)\)
Chiều cao hình bình hành sau khi tăng là:
\(189:7=27\left(m\right)\)
Diện tích ban đầu là:
\(47\cdot27=1269\left(m^2\right)\)
Đáp số: \(1269m^2\)

a: \(\left|x+\dfrac{1}{2}\right|>=0\forall x\)
Dấu '=' xảy ra khi \(x+\dfrac{1}{2}=0\)
=>\(x=-\dfrac{1}{2}\)
b: \(\left|x-\dfrac{1}{3}\right|>=0\forall x\)
=>\(\left|x-\dfrac{1}{3}\right|+2>=2\forall x\)
Dấu '=' xảy ra khi \(x-\dfrac{1}{3}=0\)
=>\(x=\dfrac{1}{3}\)
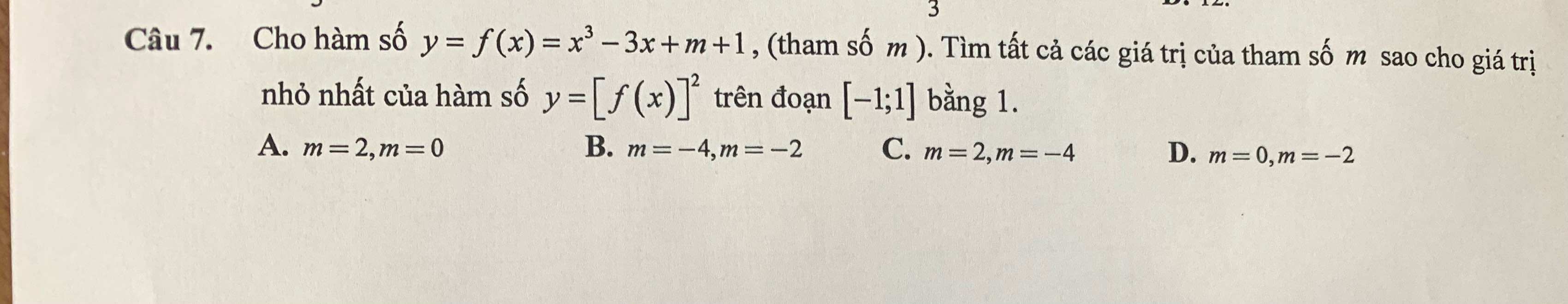

\(\dfrac{1}{1\times3}+\dfrac{1}{3\times5}+\dfrac{1}{5\times7}+...+\dfrac{1}{2007\times2009}+\dfrac{1}{2009\times2011}\\ =\dfrac{1}{2}\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{2007\times2009}+\dfrac{2}{2009\times2011}\right)\\ =\dfrac{1}{2}\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+...-\dfrac{1}{2009}+\dfrac{1}{2009}-\dfrac{1}{2011}\right)\\ =\dfrac{1}{2}\times\left(1-\dfrac{1}{2011}\right)\\ =\dfrac{1}{2}\times\dfrac{2010}{2011}\\ =\dfrac{1005}{2011}\)