\(\dfrac{a}{c}=\dfrac{a+b}{c+d}=\dfrac{a+b-a}{c+d-c}=\dfrac{b}{d}\) (T/c dãy tỷ số bằng nhau)

\(\Rightarrow\dfrac{a}{b}=\dfrac{c}{d}\) (đpcm)

$\frac{a}{b}=\frac{c}{d}$

$\Rightarrow \frac{b}{a}=\frac{d}{c}$

$\Rightarrow \frac{b}{a}-1=\frac{d}{c}-1$

$\Rightarrow \frac{b-a}{a}=\frac{d-c}{c}\Rightarrow -\left(\frac{b-a}{a}\right)=-\left(\frac{d-c}{c}\right)$

$\Rightarrow \frac{a-b}{a}=\frac{c-d}{c}\left(đpcm\right)$

A B M C D I H

a/

Xét tg CMA và tg BMD có

M là trung điểm BC => MC=MB

MA=MD (gt)

\(\widehat{AMC}=\widehat{BMD}\) (góc đối đỉnh)

=> tg CMA = tg BMD (c.g.c) (đpcm)

=> AC=BD (đpcm)

b/

Ta có

tg CMA = tg BMD (cmt) \(\Rightarrow\widehat{MAC}=\widehat{MDB}\) 

Mà hai gó trên ở vị trí so le trong => AC//BD (đpcm)

c/ Nối M với I và M với H

Xét tg AMH và tg DMI có

AH=DI (gt)

\(\widehat{MAC}=\widehat{MDB}\) (cmt)

tg CMA = tg BMD (cmt) => MA=MD

=> tg AMH = tg DMI (c.g.c) (đpcm)

Ta có

\(\widehat{DMI}+\widehat{AMI}=\widehat{AMD}=180^o\)

Mà tg AMH = tg DMI (cmt) \(\Rightarrow\widehat{DMI}=\widehat{AMH}\)

\(\Rightarrow\widehat{AMH}+\widehat{AMI}=\widehat{IMH}=180^o\)

=> I; H; M thẳng hàng (đpcm)

Gọi số học sinh giỏi ; khá ; trung bình lần lượt là a;b;c

theo bài ra ta có :

a/2=b/3=c/5

a/2+b/3+c/5=a+b+c/2+3+5

                   = 180/10=18

       a/2=18 suy ra a=18.2=36

        b/3=18 suy ra b=18.3=54

         c/5=18 suy ra c=18.5=90

Vậy ....

Mình ko nhớ cách trình bày bạn ạ

Lời giải:
Gọi số hsg, hsk, hstb lần lượt là $a,b,c$. Theo bài ra ta có:

$\frac{a}{2}=\frac{b}{3}=\frac{c}{5}$

$a+b+c=180$

Áp dụng tính chất dãy tỉ số bằng nhau:

$\frac{a}{2}=\frac{b}{3}=\frac{c}{5}=\frac{a+b+c}{2+3+5}=\frac{180}{10}=18$

$\Rightarrow a=18.2=36; b=18.3=54; c=18.5=90$ (học sinh)

Từ sau bạn viết đề cẩn thận hơn nhé.

x A y B C M

a) Do AB = AC nên tam giác ABC là tam giác cân, do đó \(\widehat{ABC}=\widehat{ACB}\) (đpcm)

b) Xét hai tam giác AMB và AMC có:

AB = AC (giả thiết)

MB = MC (giả thiết)

AM chung

Suy ra \(\Delta AMB=\Delta AMC\) (c.c.c) (đpcm)

Mình gợi ý nhé

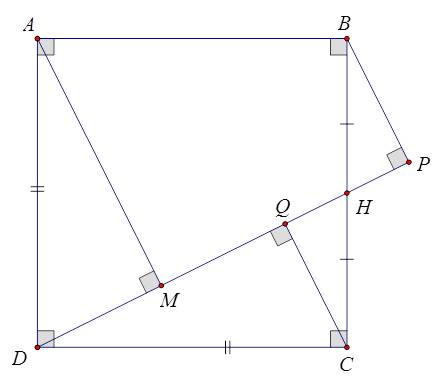
a) Hai tam giác vuông này có hai góc QHC và BHP bằng nhau (đối đỉnh); hai góc HQC và HPB bằng nhau (90^o) nên suy ra hai góc QCH và HBP cũng bằng nhau.

Từ đây chứng minh được \(\Delta QHC=\Delta PHB\left(g.c.g\right)\)

b) \(\widehat{DAM}=90^\circ-\widehat{ADM}=\widehat{QDC}=90^\circ-\widehat{QCD}=\widehat{QCH}\)

c) Từ câu b) suy ra \(\Delta DAM=\Delta CDQ\) (g.c.g) nên DM = CQ.

`(1)^2+x=3/4`

`1+x=3/4`

`x=3/4-1`

`x=-1/4`

`15-3|x|=-30`

`=>3|x|=15+30=45`

`=>|x|=15`

`=>x=15` hoặc `x=-15`

3^4-x=27

3^4-x=3^3

=> 4-x=3

x=4-3

x=1

Vậy x=1

(3)^4-x=(3)³ 
==> 4-x=3
=>x=1

điên à