\(x\) ⋮ 5; \(x\) ⋮ 4; \(x⋮\) 8; - 20 < \(x\) < 180

⇒ \(x\) BC(4; 5; 8)

4 = 2²; 5 = 5; 8 = 2³; BCNN(4;5;8) = 2³.5 = 40

⇒ \(x\) \(\in\) {0; 40; 80; 120; 160; 200; ...;}

Vì -20 < \(x\) < 180 nên \(x\) \(\in\) {0; 40; 80; 120; 160; 200}

\(2^{x+1}.3^x-6^x=216\)

\(\Leftrightarrow2^x2.3^x-2^x.3^x=216\)

\(\Leftrightarrow\left(2.3\right)^x\left(2-1\right)=216\)

\(\Leftrightarrow6^x=216\)

\(\Leftrightarrow6^x=6^3\)

\(\Leftrightarrow x=3\)

\(2^{x+1}.3^x-6^x=216\)

\(=>2^x.2.3^x-6^x=216\)

\(=>\left(2.3\right)^x.2-6^x=216\)

\(=>6^x.2-6^x=216\)

\(=>6^x.\left(2-1\right)=216\)

\(=>6^x.1=216\)

\(=>6^x=216:1=216\)

\(=>6^x=6^3\)

\(=>x=3\)

Vậy...

\(#NqHahh\)

10231000000000000000000

\(3^x-3^{x+3}=-234\)

\(=>3^x-3^x.3^3=-234\)

\(=>3^x.\left(1-3^3\right)=-234\)

\(=>3^x.\left(1-27\right)=-234\)

\(=>3^x.-26=-234\)

\(=>3^x=\left(-234\right):\left(-26\right)\)

\(=>3^x=9=3^2\)

\(=>x=2\)

\(#NqHahh\)

3^x-3^x.27=-234

3^x.(1-27)=-234

3^x.(-26)=-234

3^x=234:26

3^x=9

=>3^x=3^3

Bạn kiểm tra đề nha.

Đề bài sai. Bạn xem lại.

Vì ABC là tam giác đều

Nên AB=AC=BC

=> AC=10 cm

=> Chọn A

what

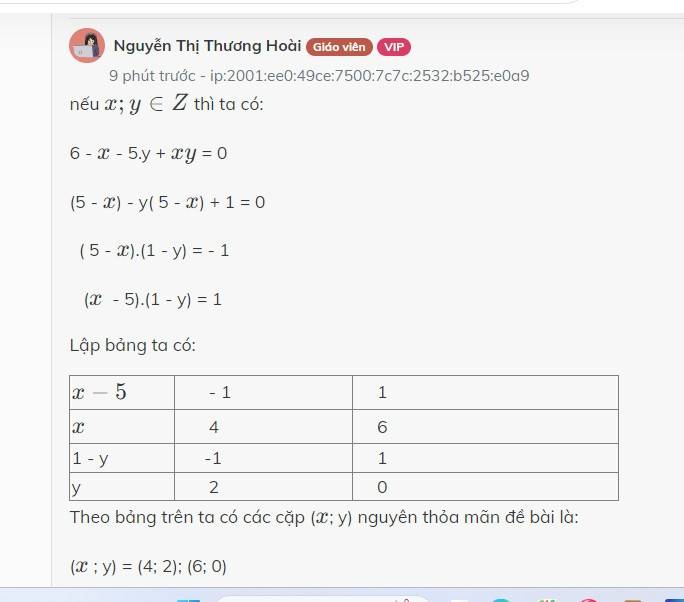
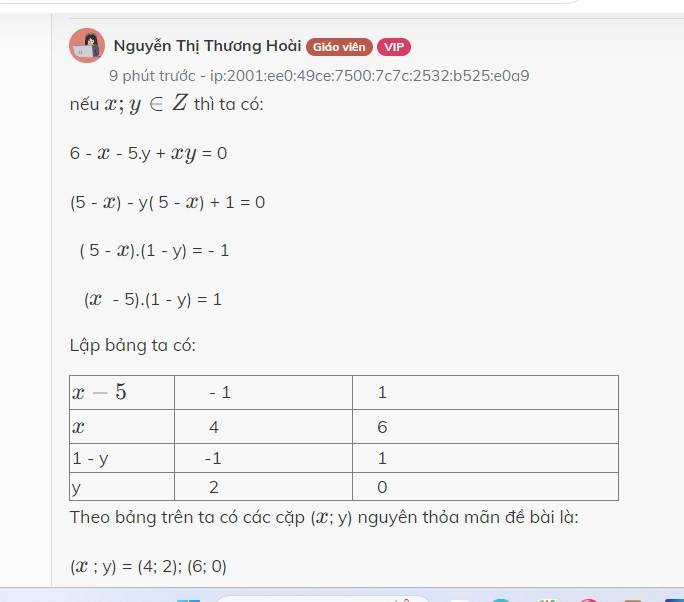
nếu \(x;y\in Z\) thì ta có:

6 - \(x\) - 5.y + \(xy\) = 0

(5 - \(x\)) - y( 5 - \(x\)) + 1 = 0 

  ( 5 - \(x\)).(1 - y) = - 1

   (\(x\)  - 5).(1 - y) = 1

Lập bảng ta có: 

Theo bảng trên ta có các cặp (\(x\); y) nguyên thỏa mãn đề bài là:

(\(x\) ; y) = (4; 2); (6; 0)

Ta có:

 \(BCNN\left(12,21,28\right)=84\)

\(\Rightarrow x\in BC\left(84\right)=\left\{0,84,168,252,336,420,...\right\}\)

Mà \(150< x< 300\)

\(\Rightarrow\left[{}\begin{matrix}x=168\\x=252\end{matrix}\right.\)

⇒ BCNN(12; 21; 28) = 22.3.7 = 84. ⇒ x ∈ BC(12; 21; 28) = B(84) = {0; 84; 168; 252; 336; 420; …}. Vì 150 < x < 300 nên x = 168 hoặc x = 252.

Bình quân mỗi tháng công lãi hoặc lỗ số tiền từ ba cửa hàng là: 380 + (-250) + 340 = 470(triệu đồng) ⇒ Công ty lãi 470 triệu động từ 3 cửa hàng đó.

Đ/số:...