a: Xét ΔMNQ có

NE,MF là các đường cao

NE cắt MF tại H

Do đó: H là trực tâm của ΔMNQ

=>QH\(\perp\)MN tại D

Xét `ΔMQN` có: 

Đường cao `NE` và `MF` cắt nhau tại H

`=> H` là trực tâm của `ΔMQN`

`=> QD` là đường cao của `ΔMQN` (đi qua H)

`=> QH  MN` tại `D`

Với mọi x;y dương ta có:

\(x^2+xy+y^2=\dfrac{3}{4}\left(x^2+2xy+y^2\right)+\dfrac{1}{4}\left(x^2-2xy+y^2\right)\)

\(=\dfrac{3}{4}\left(x+y\right)^2+\dfrac{1}{4}\left(x-y\right)^2\ge\dfrac{3}{4}\left(x+y\right)^2\)

Áp dụng:

\(P\ge\sqrt{\dfrac{3}{4}\left(a+b\right)^2}+\sqrt{\dfrac{3}{4}\left(b+c\right)^2}+\sqrt{\dfrac{3}{4}\left(c+a\right)^2}\)

\(P\ge\dfrac{\sqrt{3}}{2}\left(a+b\right)+\dfrac{\sqrt{3}}{2}\left(b+c\right)+\dfrac{\sqrt{3}}{2}\left(c+a\right)\)

\(P\ge\sqrt{3}\left(a+b+c\right)=\sqrt{3}\)

\(P_{min}=\sqrt{3}\) khi \(a=b=c=\dfrac{1}{3}\)

a: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)

=>\(1-\dfrac{AB'}{AB}=1-\dfrac{AC'}{AC}\)

=>\(\dfrac{BB'}{AB}=\dfrac{CC'}{AC}\)

=>\(\dfrac{BB'}{CC'}=\dfrac{AB}{AC}\)

mà \(\dfrac{AB}{AC}=\dfrac{AB'}{AC'}\)

nên \(\dfrac{AB'}{AC'}=\dfrac{BB'}{CC'}\)

=>\(\dfrac{AB'}{BB'}=\dfrac{AC'}{CC'}\)

b: \(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)

=>\(1-\dfrac{AB'}{AB}=1-\dfrac{AC'}{AC}\)

=>\(\dfrac{BB'}{AB}=\dfrac{CC'}{AC}\)

a: Thay m=3 vào hệ, ta được:

\(\left\{{}\begin{matrix}3x+2y=1\\3x+\left(3+1\right)y=-1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3x+2y=1\\3x+4y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3x+4y-3x-2y=-1-1\\3x+2y=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}2y=-2\\3x=1-2y=1-\left(-2\right)=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=-1\\x=1\end{matrix}\right.\)

b:

để hệ có vô số nghiệm thì \(\dfrac{m}{3}=\dfrac{2}{m+1}=\dfrac{1}{-1}\)

=>\(\left\{{}\begin{matrix}m^2+m=6\\m+1=-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m+3\right)\left(m-2\right)=0\\m=-3\end{matrix}\right.\)

=>m=-3

Để hệ vô nghiệm thì \(\dfrac{m}{3}=\dfrac{2}{m+1}\ne\dfrac{1}{-1}=-1\)

=>\(\left\{{}\begin{matrix}m^2+m=6\\m+1\ne-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\left(m+3\right)\left(m-2\right)=0\\m\ne-3\end{matrix}\right.\)

=>m=2

Để hệ có nghiệm duy nhất thì \(\dfrac{m}{3}\ne\dfrac{2}{m+1}\)

=>\(m^2+m\ne6\)

=>\(m^2+m-6\ne0\)

=>(m+3)(m-2)<>0

=>\(m\notin\left\{-3;2\right\}\)

\(\left\{{}\begin{matrix}mx+2y=1\\3x+\left(m+1\right)y=-1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}3mx+6y=3\\3mx+\left(m^2+m\right)y=-m\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}3mx+\left(m^2+m\right)y-3mx-6y=-m-3\\mx+2y=1\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y\left(m+3\right)\left(m-2\right)=-\left(m+3\right)\\mx+2y=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=\dfrac{-1}{m-2}\\mx=1-2y=1+\dfrac{2}{m-2}=\dfrac{m-2+2}{m-2}=\dfrac{m}{m-2}\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}y=-\dfrac{1}{m-2}\\x=\dfrac{1}{m-2}\end{matrix}\right.\)

c: Để hệ có nghiệm duy nhất là số nguyên thì \(\left\{{}\begin{matrix}m\in\left\{-3;2\right\}\\m-2\inƯC\left(1;-1\right)\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m\in\left\{-3;2\right\}\\m-2\in\left\{1;-1\right\}\end{matrix}\right.\)

=>\(m\in\left\{3;1\right\}\)

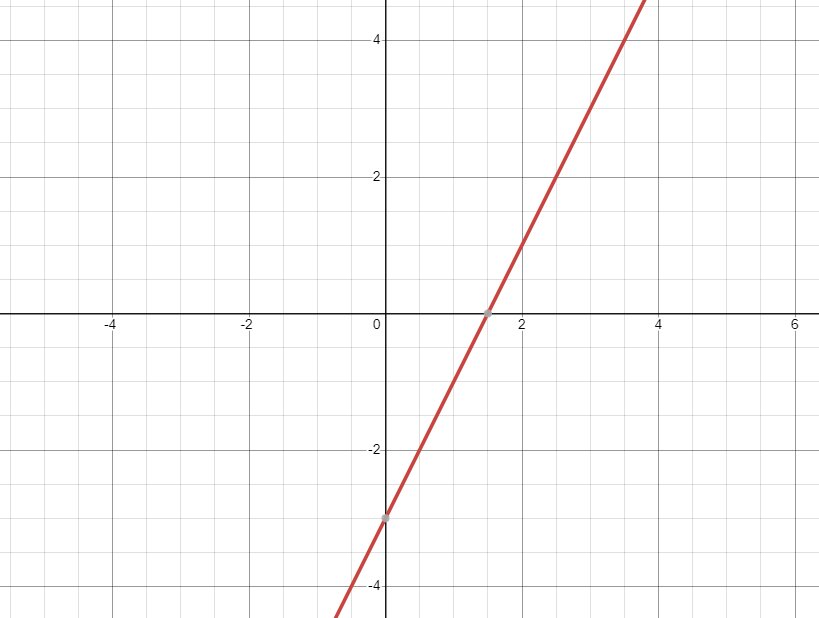
Đồ thị hàm số cắt Ox tại: `(3/2;0)`

Đồ thị hàm số cắt Oy tại `(0;-3)

Vẽ đồ thị hàm số: 

Gọi số km di chuyển được là x

\(\Rightarrow17+15.x\le300\)

\(\Rightarrow x\le18,9\left(km\right)\)

Vậy hành khách di chuyển được tối đa 18,9km

Gọi \(x>0\left(km\right)\) là số km tiếp theo

Theo đề bài ta có :

\(17000+15000x=300000\)

\(\Leftrightarrow15000x=283000\)

\(\Leftrightarrow x=\dfrac{283000}{15000}\approx19\left(km\right)\)

Vậy với \(300000\) thì hành khách có thể đi tối đa \(19\left(km\right)\)

Gọi số đó là \(\overline{xy}\) (với x;y là các chữ số từ 0 tới 9, `x \neq 0`)

Do tổng 2 chữ số bằng 9 nên: \(x+y=9\) (1)

Số mới sau khi viết thêm chữ số 0 vào giữa: \(\overline{x0y}\)

Do số mới gấp 9 lần số cũ nên:

\(\overline{x0y}=9\overline{xy}\Leftrightarrow100x+y=9\left(10x+y\right)\)

\(\Leftrightarrow10x-8y=0\) (2)

Từ (1) và (2) ta có hệ: \(\left\{{}\begin{matrix}x+y=9\\10x-8y=0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x=4\\y=5\end{matrix}\right.\)

Vậy số đó là 45

Gọi số đó là `overline{ab} (a ne 0)`

`=> overline{a0b} = 9 . overline{ab}`

`=> b ∈ {0; 5}`

Xét `b = 0`

thì: `overline{a0} . 9 = overline{a00}`

`=> overline{a0} = overline{a00} : 9`

Hay `overline{a00} vdots 9`

`<=> a + 0 + 0 vdots 9`

`<=> a = 9`

Khi đó:  `overline{a00} : 9 = 900 : 9 = 100` (không thỏa mãn)

Xét `b = 5`

thì: `overline{a5} . 9 = overline{a05}`

`=> overline{a5} = overline{a05} : 9`

Hay `overline{a05} vdots 9`

`<=> a + 0 + 5 vdots 9`

`<=> a = 4`

Khi đó:  `overline{a05} : 9 = 405 : 9 = 45` (Thỏa mãn)

Vậy số đó là `45`