Cho tam giác ABC, vẽ điểm M là trung điểm của BC. Trên tia đối của tia MA lấy điểm D sao cho MA = MD.c)Kẻ AH vuông góc với BC, DK vuông góc BC (H,K thuộc BC). Chứng minh BK=CH d)Gọi I là trung điểm của AC, vẽ điểm E sao cho I là trung điểm của BE. Chứng minh C là trung điểm của DE
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D I E M
a/
Ta có
\(\widehat{EAD}=\widehat{BAI}\) (góc đối dỉnh)
\(\widehat{IAC}=\widehat{BAI}\left(gt\right)\)
\(\Rightarrow\widehat{EAD}=\widehat{IAC}\)
Xét tg EAD và tg IAC có
\(\widehat{EAD}=\widehat{IAC}\left(cmt\right)\)
AE=AI (gt); AD=AC (gt)
=> tg EAD = tg IAC (c.g.c)\(\Rightarrow\widehat{ADE}=\widehat{ACI}\)
b/
Xét tg ACD có
AD=AC (gt) => tg ACD cân tại A
Ta có
MD=MC (gt)
\(\Rightarrow\widehat{MAD}=\widehat{MAC}\) (trong tg cân đường trung tuyến xuất phát từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh tg cân)
Ta có
tg EAD = tg IAC (cmt) \(\Rightarrow\widehat{EAD}=\widehat{IAC}\)
\(\Rightarrow\widehat{MAD}+\widehat{EAD}=\widehat{MAC}+\widehat{IAC}\)
\(\Rightarrow\widehat{MAE}=\widehat{MAI}\)
Mà \(\widehat{MAE}+\widehat{MAI}=\widehat{EAI}=180^o\Rightarrow\widehat{MAE}=\widehat{MAI}=90^o\Rightarrow AM\perp AI\)
c/
\(AM\perp AI\Rightarrow AM\perp IE\) (1)
Xét tg cân ACD có
MD=MC (gt)
\(\Rightarrow AM\perp CD\) (trong tg cân đường trung tuyến xp từ đỉnh tg cân đồng thời là đường cao) (2)
Từ (1) và (2) => IE//CD (cùng vuông góc với AM)

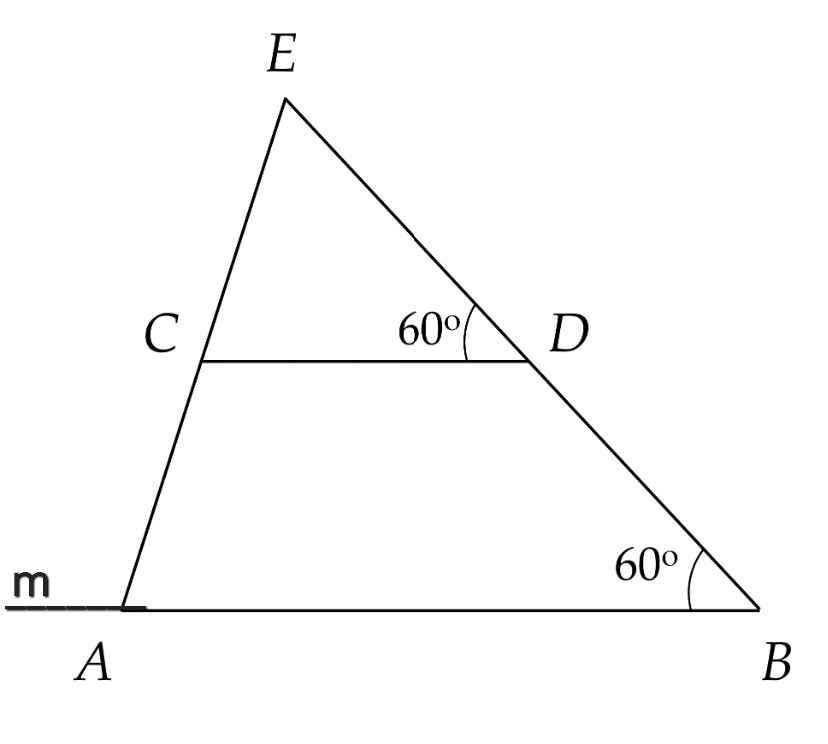
a) Ta có:
∠ABD = ∠CDE = 60⁰ (gt)
Mà ∠ABD và ∠CDE là hai góc so le trong
⇒ AB // CD
b) Vẽ tia Am là tia đối của tia AB
Do AB // CD
⇒ ∠mAC = ∠ACD (so le trong)
Mà ∠mAC + ∠BAC = 180⁰ (kề bù)
⇒ ∠ACD + ∠BAC = 180⁰

2/3 - |x - 1/2| = 2/3
|x - 1/2| = 2/3 - 2/3
|x - 1/2| = 0
x - 1/2 = 0
x = 0 + 1/2
x = 1/2

11/3 . 2/5 + 11/3 . 8/5 - 11/3
= 11/3 . (2/5 + 8/5 - 1)
= 11/3 . (2 - 1)
= 11/3 . 1
= 11/3


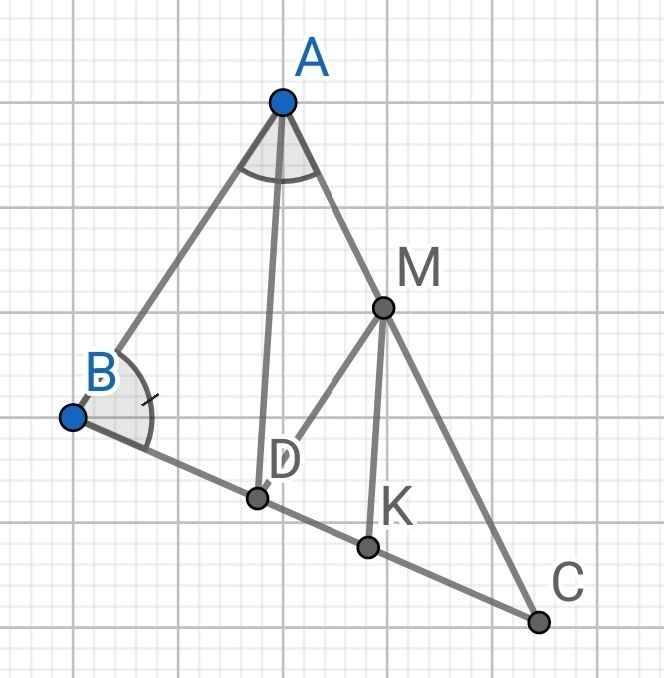
Do AD là tia phân giác của ∠BAC (gt)
⇒ ∠BAD = ∠DAM = 60⁰ : 2 = 30⁰
Do DM // AB (gt)
⇒ ∠ADM = ∠BAD = 30⁰ (so le trong)
Do DM // AB (gt)
⇒ ∠MDK = ∠B = 80⁰ (đồng vị)
⇒ ∠ADK = ∠ADM + ∠MDK
= 30⁰ + 80⁰
= 110⁰

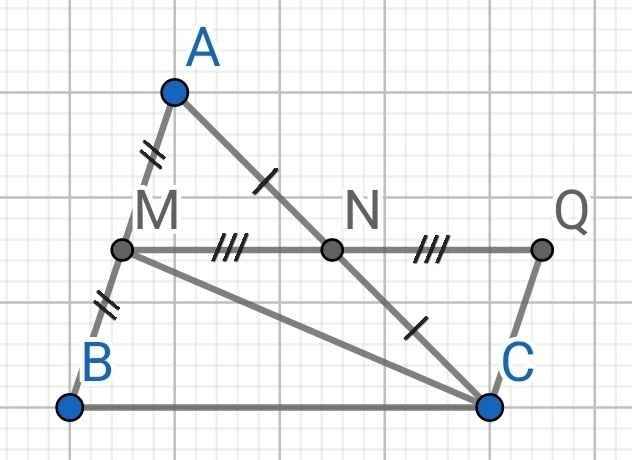
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC

Đổi: 15cm=1,5dm
Thể tích bể cá khi chưa thả hòn đá vào là:
5x12x7=420(dm3)
Thể tích bể cá khi thả hòn đá vào là:
5x12x(7+1,5)=510 (dm3)
Thể tích hòn đá là:
510-420=90 (dm3)
Đáp số:90 dm3
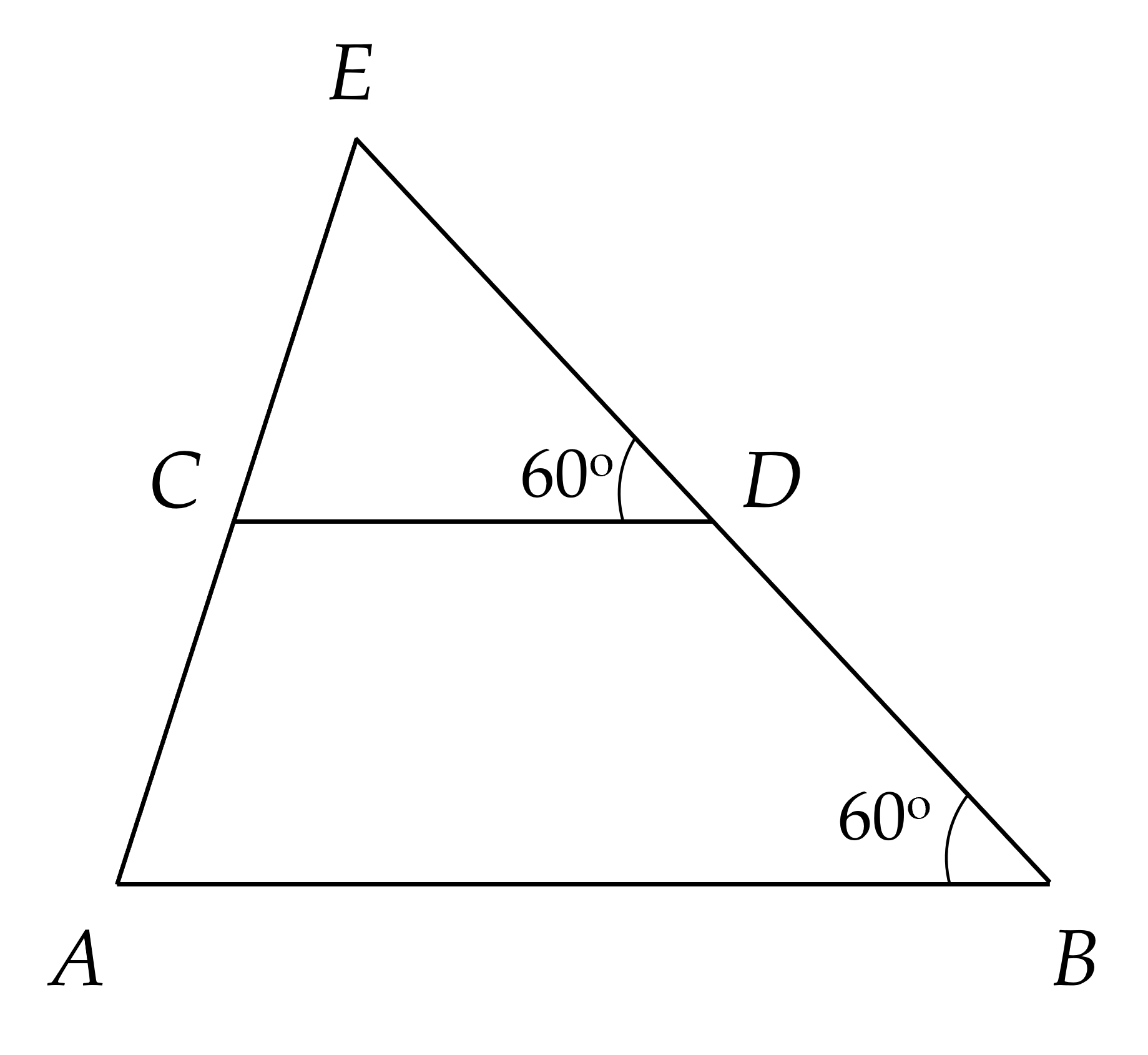
⇒ BM = MC
Xét hai tam giác vuông: ∆AHM và ∆DKM có:
MA = MD (gt)
∠AMH = ∠DMK (đối đỉnh)
⇒ ∆AHM = ∆DKM (cạnh huyền - góc nhọn)
⇒ HM = KM (hai cạnh tương ứng)
Ta có:
BK = BM + KM
CH = CM + HM
Mà BM = CM (cmt)
KM = HM (cmt)
⇒ BK = CH
d) Tứ giác ABDC có:
M là trung điểm của BC (gt)
M là trung điểm của AD (gt)
⇒ ABDC là hình bình hành
⇒ AB // DC và AB = DC
Tứ giác ABCE có:
I là trung điểm của AC (gt)
I là trung điểm của BE (gt)
⇒ ABCE là hình bình hành
⇒ AB // CE và AB = CE
Do AB // CE (cmt)
AB // DC (cmt)
⇒ C, D, E thẳng hàng (theo tiên đề Ơ-clít)
Ta có:
AB = CE (cmt)
AB = DC (cmt)
⇒ CD = CE
⇒ C là trung điểm của DE