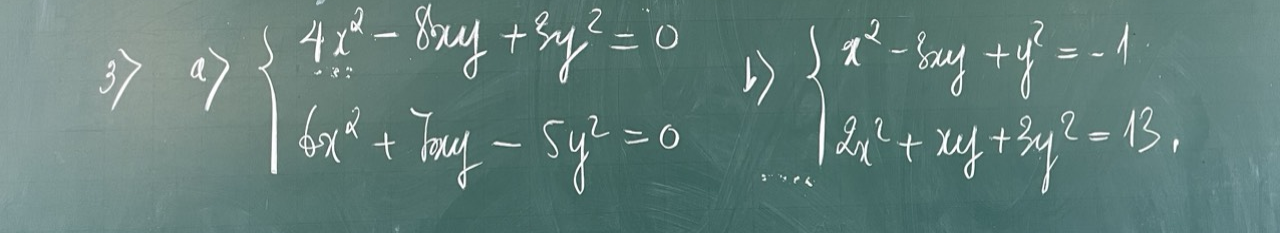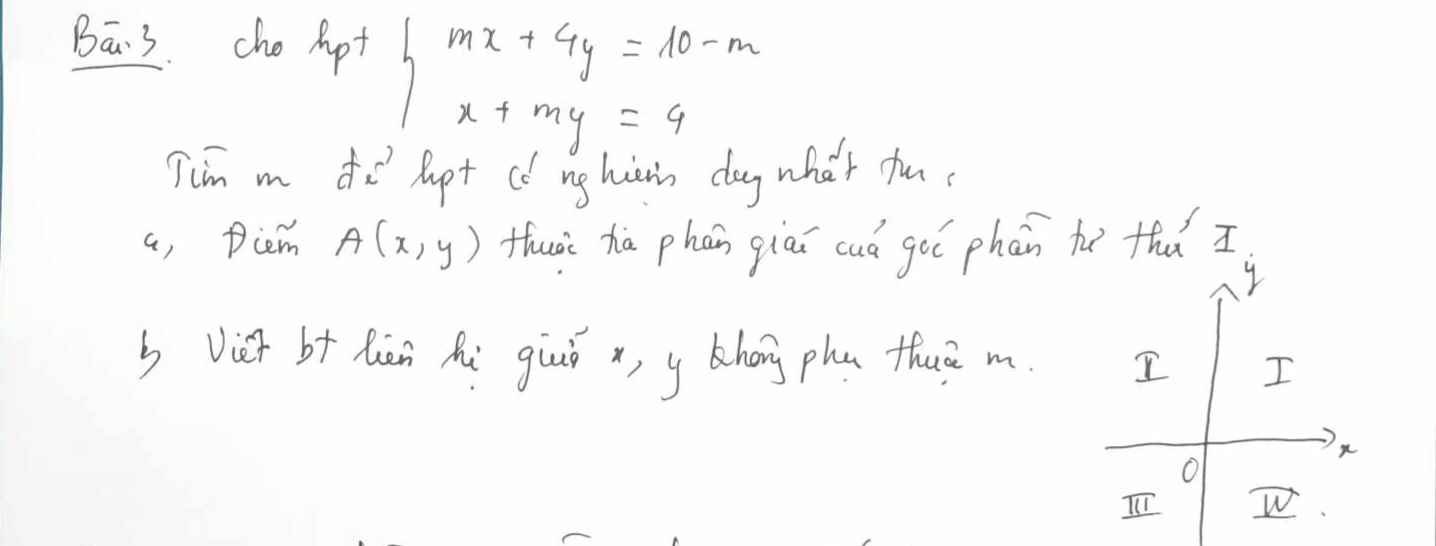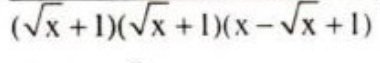1 You are not allowed to drive if you don’t have a driving license
2 In spite of the heavy rain, he went out without a raincoat
3 We have been married for 10 years

a.

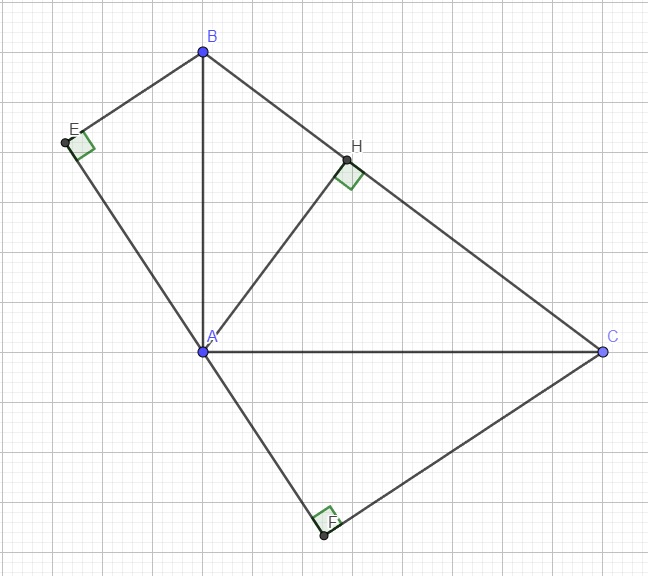
Ta có: \(\widehat{BAE}+\widehat{BAC}+\widehat{CAF}=180^0\)

\(\Rightarrow\widehat{BAE}+90^0+\widehat{CAF}=180^0\)

\(\Rightarrow\widehat{BAE}+\widehat{CAF}=90^0\) (1)

Lại có \(BE\perp d\Rightarrow\Delta BAE\) vuông tại E

\(\Rightarrow\widehat{BAE}+\widehat{ABE}=90^0\) (2)

(1);(2) \(\Rightarrow\widehat{CAF}=\widehat{ABE}\)

Xét hai tam giác ABE và CAF có:

\(\left\{{}\begin{matrix}\widehat{ABE}=\widehat{CAF}\\\widehat{AEB}=\widehat{CFA}=90^0\end{matrix}\right.\)

\(\Rightarrow\Delta ABE\sim\Delta CAF\left(g.g\right)\)

\(\Rightarrow\dfrac{AE}{CF}=\dfrac{BE}{AF}\Rightarrow AE.AF=BE.CF\)

b.

\(S_{ABC}=\dfrac{1}{2}AB.AC\Rightarrow AC=\dfrac{2S_{ABC}}{AB}=\dfrac{2.24}{6}=8\left(cm\right)\)

Áp dụng hệ thức lượng:

\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\Rightarrow AH=\dfrac{AB.AC}{\sqrt{AB^2+AC^2}}=\dfrac{6.8}{\sqrt{6^2+8^2}}=4,8\left(cm\right)\)

Gọi số cần tìm là \(\overline{xy}\) với x;y là các chữ số từ 0 tới 9, `x \ne 0`

Do tổng chữ số hàng chục và 2 lần chữ số hàng đơn vị là 12 nên ta có:

\(x+2y=12\) (1)

Sau khi thêm chữ số 0 vào giữa ta được số mới là: \(\overline{x0y}\)

Do số mới hơn số cũ 180 đơn vị nên ta có pt:

\(\overline{x0y}-\overline{xy}=180\Leftrightarrow100x+y-\left(10x+y\right)=180\)

\(\Leftrightarrow90x=180\)

\(\Leftrightarrow x=2\)

Thay vào (1) \(\Rightarrow2+2y=12\Rightarrow y=5\)

Vậy số đó là 25

a.

\(\Leftrightarrow\left\{{}\begin{matrix}\left(2x-3y\right)\left(2x-y\right)=0\\6x^2+7xy-5y^2=0\end{matrix}\right.\)

TH1: \(2x-3y=0\Rightarrow y=\dfrac{2}{3}x\) thay vào pt dưới

\(\Rightarrow6x^2+7x.\left(\dfrac{2}{3}x\right)-5\left(\dfrac{2}{3}x\right)^2=0\)

\(\Leftrightarrow\dfrac{76}{9}x^2=0\Rightarrow x=0\Rightarrow y=0\)

TH2: \(2x-y=0\Rightarrow y=2x\)

Tương tự ta cũng được \(x=0;y=0\)

Vậy hệ có nghiệm duy nhất \(\left(x;y\right)=\left(0;0\right)\)

b.

\(\Leftrightarrow\left\{{}\begin{matrix}13x^2-39xy+13y^2=-13\\2x^2+xy+3y^2=13\end{matrix}\right.\)

Cộng vế với vế

\(\Rightarrow15x^2-38xy+16y^2=0\)

\(\Leftrightarrow\left(x-2y\right)\left(15x-8y\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=2y\\x=\dfrac{8}{15}y\end{matrix}\right.\)

Thay vào pt đầu:

- Với \(x=2y\Rightarrow4y^2-6y^2+y^2=-1\)

\(\Rightarrow y^2=1\Rightarrow\left[{}\begin{matrix}y=1\Rightarrow x=2\\y=-1\Rightarrow x=-2\end{matrix}\right.\)

- Với \(x=\dfrac{8}{15}y\)

\(\Rightarrow\left(\dfrac{8}{15}y\right)^2-3\left(\dfrac{8}{15}y\right).y+y^2=-1\)

\(\Leftrightarrow-\dfrac{71}{225}y^2=-1\Rightarrow y^2=\dfrac{225}{71}\)

\(\Rightarrow\left[{}\begin{matrix}y=\dfrac{15}{\sqrt{71}}\Rightarrow x=\dfrac{8}{\sqrt{71}}\\y=-\dfrac{15}{\sqrt{71}}\Rightarrow x=-\dfrac{8}{\sqrt{71}}\end{matrix}\right.\)

Em để ý thấy 2 số hạng đầu nếu đặt \(x\sqrt{x}\) làm nhân tử chung được: \(x\sqrt{x}\left(\sqrt{x}+1\right)\)

Giờ nó lại xuất hiện nhân tử \(\sqrt{x}+1\) với 2 số hạng cuối

Cứ vậy là ra thôi

Đề yêu cầu chứng minh hay tìm \(x;y\) vậy em nhỉ?

- Kiều Nguyệt Nga là một cô gái kiêu sa, dịu dàng, hiểu biết, và lòng trọng ân nghĩa. - Nhân vật này thể hiện lòng biết ơn, lòng chân thành, và tư tưởng đền ơn báo nghĩa. - Kiều Nguyệt Nga là hình mẫu của người con gái truyền thống, nết na, hiền thục, và có hiểu biết.

@quocbao chép trên mạng thì có cái ích giề?