Tìm tất cả các cặp số \(a,b\inℕ\) để \(\sqrt{a}+\sqrt{b}=\sqrt{2009}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Ta có: \(y=\dfrac{x+5}{x+2}=\dfrac{x+2+3}{x+2}=1+\dfrac{3}{x+2}\)
Do \(x\in Z\), để \(y\in Z\) thì \(\left(x+2\right)\inƯ\left(3\right)=\left\{\pm1;\pm3\right\}\)
Nếu \(x+2=1\Rightarrow x=-1\)
Nếu \(x+2=-1\Rightarrow x=-3\)
Nếu \(x+2=3\Rightarrow x=1\)
Nếu \(x+2=-3\Rightarrow x=-5\)
Vậy \(x\in\left\{1;-1;-3;-5\right\}\)
Điều kiện \(x\ne-2\)
Ta có \(y=\dfrac{x+5}{x+2}=\dfrac{x+2+3}{x+2}=1+\dfrac{3}{x+2}\)
Do \(1\inℤ\) nên để \(y\inℤ\) thì \(\dfrac{3}{x+2}\inℤ\) hay \(3⋮\left(x+2\right)\) hay \(\left(x+2\right)\inƯ\left(3\right)\) hay \(\left(x+2\right)\in\left\{\pm1;\pm3\right\}\)
Với \(x+2=1\Leftrightarrow x=-1\left(nhận\right)\)
\(x+2=-1\Leftrightarrow x=-3\left(nhận\right)\)
\(x+2=3\Leftrightarrow x=1\left(nhận\right)\)
\(x+2=-3\Leftrightarrow x=-5\left(nhận\right)\)
Vậy \(x\in\left\{-3;-5;-1;1\right\}\)

giả sử tồn tại n ϵ N* để
5n-1 + 7n-1 ⋮ 5n +7n
⇔ 35 (5n-1 + 7n-1) ⋮ 5n + 7n
⇔ 7.5n + 7n.5 ⋮ 5n + 7n
⇔ 7. (5n + 7n) - 2.7n ⋮5n +7n
⇔2.7n ⋮ 5n + 7n
⇔2.7n = 5n + 7n
⇔ 7n = 5n
⇔ n = 0 (loại)
vậy không có giá trị nào của n ϵ N* thỏa mãn đề bài

4.2sina2cosa2.2sina2cosa21−cos2a2=16sin2a2cos2a21−cos2a2VT=4sina.sina1−cos2a2=4.2sina2cosa2.2sina2cosa21−cos2a2=16sin2a2cos2a21−cos2a2=16sin2a2cos2a21−(1−sin2a2)=16sin2a2cos2a2sin2a2=16cos2a2




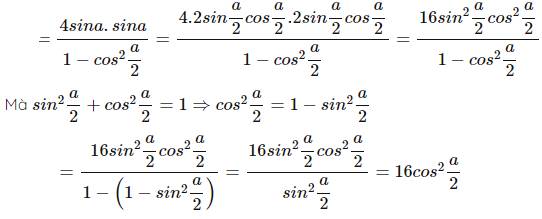



\(a;b\ge0\)
\(\sqrt{b}=\sqrt{2009}-\sqrt{a}\)
BP 2 vế
\(b=2009+a+2\sqrt{2009.a}\)
\(\Rightarrow\sqrt{2009.a}\) là số nguyên
\(\sqrt{2009.a}=\sqrt{41.49.a}=7\sqrt{41.a}\)
\(\Rightarrow\sqrt{41.a}\) là số nguyên => a có dạng \(a=41.m^2\)
Tương tự ta cũng có b có dạng \(b=41.n^2\)
Trong đó \(m;n\in N\)
\(\Rightarrow\sqrt{a}+\sqrt{b}=\sqrt{41m^2}+\sqrt{41n^2}=\sqrt{41.49}=7\sqrt{41}\)
\(\Rightarrow m+n=7\)