Chia số học sinh này thành 3 nhóm:

- Nhóm 1: Xe thứ nhất, xe thứ sáu

- Nhóm 2: Xe thứ hai, xe thứ năm

- Nhóm 3: Xe thứ ba, xe thứ tư

Vì theo dữ kiện đề bài, thì tổng số HS xe thứ nhất và xe thứ sáu = Tống số học sinh xe thứ hai và xe thứ 5 = Tổng số học sinh xe thứ ba và xe thứ tư

Vậy, mỗi nhóm có:

330:3= 110(học sinh)

Anh dự đoán trên mỗi xe du lịch này có số học sinh bằng nhau.

Vậy số HS (có thể) có trên từng xe là:

110:2= 55(học sinh)

`(x^2+1)^2+3x(x^2+1)+2x^2=0`

`<=>(x^2+1)^2+2(x^2+1). 3/2x+9/4x^2+-1/4x^2=0`

`<=>(x^2+1+3/2x)^2-1/4x^2=0`

`<=>(x^2+1+3/2x-1/2x)(x^2+1+3/2x+1/2x)=0`

`<=>(x^2+x+1)(x^2+2x+1)=0`

`<=>[(x+1/2)^2+3/4](x+1)^2=0`

  `=>x+1=0`

`<=>x=-1`

Đổi : `22` phút `=22/60=11/30` (giờ)

Gọi độ dài quãng đường AB là : `x` (km) (x>0)

+) Thời gian đi là : \(\dfrac{x}{15}\left(h\right)\)

+) Thời gian về là : \(\dfrac{x}{12}\left(h\right)\)

Mà thời gian về nhiều hơn thời gian đi `22` phút, nên ta có phương trình :

\(\dfrac{x}{12}-\dfrac{x}{15}=\dfrac{11}{30}\\ < =>\dfrac{15x}{180}-\dfrac{12x}{180}=\dfrac{66}{180}\\ =>15x-12x=66\\ < =>3x=66\\ < =>x=22\left(TMDK\right)\)

Vậy quãng đường AB dài 22km

a)

`2x+4=x-1`

`<=>2x-x=-4-1`

`<=>x=-5`

Vậy phương trình có tập nghiệm là : \(S=\left\{-5\right\}\)

b)

`2x(x-3)-5(x-3)=0`

`<=>(x-3)(2x-5)=0`

`=>x-3=0` hoặc `2x-5=0`

`<=>x=3` hoặc `x=5/2`

Vậy tập nghiệm phương trình là : \(S=\left\{3;\dfrac{5}{2}\right\}\)

c)

\(\dfrac{2x}{x+1}=\dfrac{x^2-x+8}{\left(x+1\right)\left(x-4\right)}\left(x\ne\left\{-1;4\right\}\right)\\ < =>\dfrac{2x\left(x-4\right)}{\left(x+1\right)\left(x-4\right)}=\dfrac{x^2-x+8}{\left(x+1\right)\left(x-4\right)}\\ =>2x\left(x-4\right)=x^2-x+8\\ < =>2x^2-8x=x^2-x+8\\ < =>2x^2-x^2-8x+x-8=0\\ < =>x^2-7x-8=0\\ < =>\left(x-8\right)\left(x+1\right)=0\\ =>\left[{}\begin{matrix}x=8\left(N\right)\\x=-1\left(L\right)\end{matrix}\right.\)

Vậy tập nghiệm phương trình là : \(S=\left\{8\right\}\)

`x^2-4x+y^2-6y+15=2`

`<=>x^2-4x+4+y^2-6y+9=0`

`<=>(x-2)^2+(y-3)^2=0`

 `=>x-2=0` và `y-3=0`

`<=>x=2` và `y=3`

Ta có: 

�2−4�+�2−6�+15=2⇔�2−4�+4+�2−6�+9=0⇔(�−2)2+(�−3)2=0⇔{(�−2)2=0(�−3)2=0⇔{�=2�=3⇔⇔⇔​x2−4x+y2−6y+15=2x2−4x+4+y2−6y+9=0(x−2)2+(y−3)2=0{(x−2)2=0(y−3)2=0​⇔{x=2y=3​​

(vì (�−2)2≥0(x−2)2≥0 với mọi $x\in \mathbb{R}$, (�−3)2≥0(y−3)2≥0 với mọi $y\in \mathbb{R}$).

Vậy $x=2$, $y=3$. 

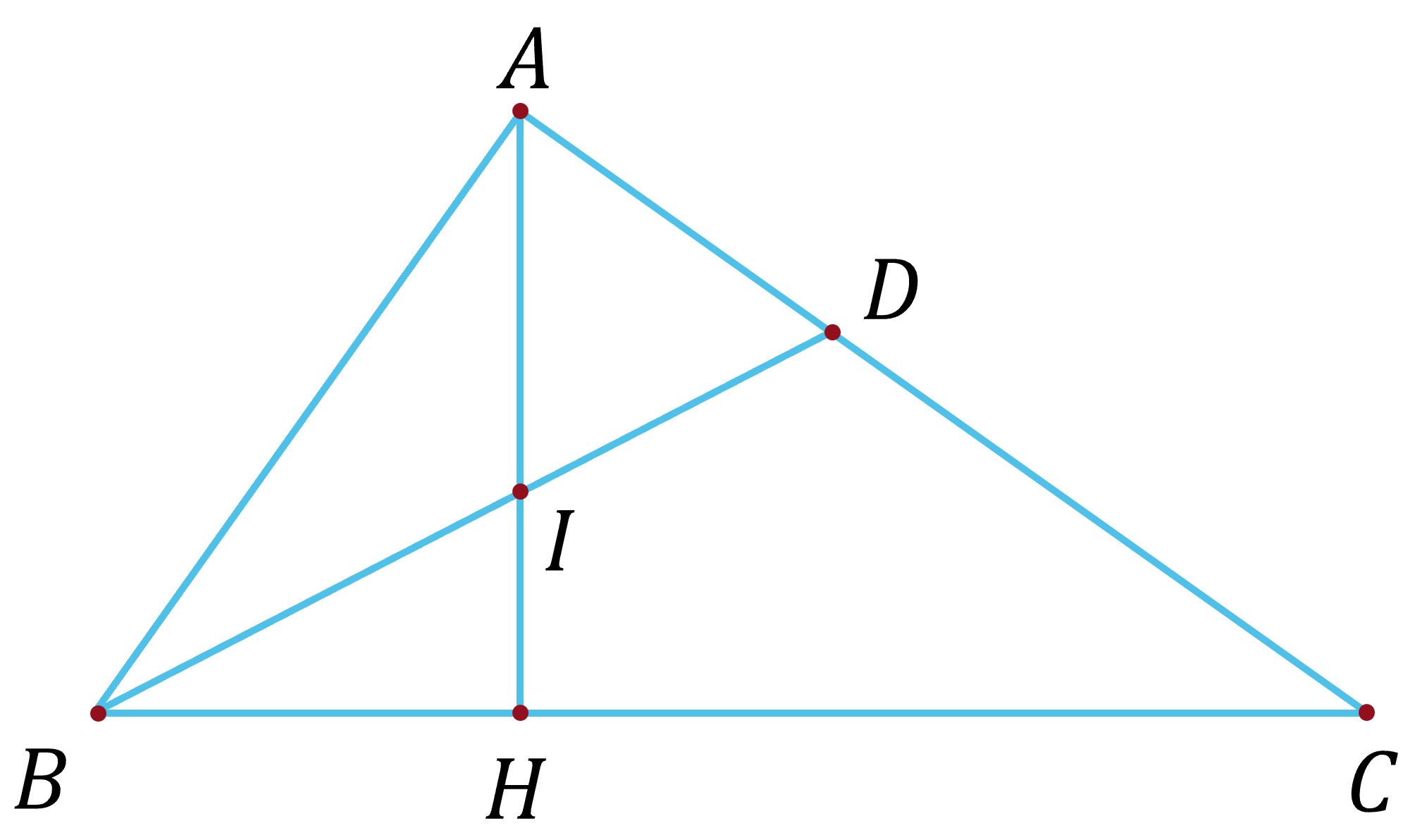
A A B C H D I

a) Vì tam giác ABC vuông tại A

Áp dụng định lý Pytago :

AB² + AC² = BC²

<=> 6² + 8² = BC²

<=> BC = 10

BD tia phân giác góc B nên \(\dfrac{AD}{DC}=\dfrac{AB}{BC}=\dfrac{3}{5}\)(1)

mà AD + DC = AC = 8 (2) 

Từ (1)(2) ta tìm được AD = 3 ; DC = 5

=> P = AD.DC = 3.5 = 15 

b) Mà \(BD\cap AH=\left\{I\right\}\)

\(\Rightarrow\dfrac{AI}{IH}=\dfrac{AB}{BH}\)(3)

Xét tam giác ABH và tam giác ABC có

\(\widehat{ABC}\) chung ; \(\widehat{AHB}=\widehat{BAC}=90^{\text{o}}\) 

nên \(\Delta CBA\sim\Delta ABH\)

\(\Rightarrow\dfrac{BH}{AB}=\dfrac{AB}{BC}\)

\(\Rightarrow\dfrac{IH}{IA}=\dfrac{AD}{DC}\)( kết hợp (1);(3))

c) Tương tự dễ thấy

\(\Delta BIH\sim\Delta BDA\) (g-g)

=> \(\widehat{BDA}=\widehat{BIH}\)

lại có \(\widehat{BIH}=\widehat{AID}\) (đối đỉnh)

nên \(\widehat{BDA}=\widehat{AID}\) => Tam giác AID cân tại A

a) Xét tam giác $ABC$ vuông tại $A$: 

��2=��2+��2BC2=AB2+AC2 (định lí Pythagoras)

⇔��2=62+82=100⇔��=10(��)⇔BC2=62+82=100⇔BC=10(cm). 

Xét tam giác $ABC$ phân giác $BD$ có: 

����=����⇔����+��=����+��BCAB​=DCAD​⇔BC+ABAB​=DC+ADAD​ 

����=����+��⇔��=3(��)ACAD​=BC+ABAB​⇔AD=3(cm)

suy ra $DC=5(cm)$.

b) Xét tam giác $ABH$ phân giác $BI$ có: ����=����IAIH​=ABHB​.

Xét $△HBA$ và $△ABC$ có: 

���^=���^HBA=ABC (góc chung)

���^=���^(=90∘)BHA=BAC(=90∘)

suy ra $△HBA\sim △ABC$ (g.g).

Suy ra ����=����ABHB​=BCBA​ 

⇒����=����⇒BCBA​=IAIH​. 

Mà ta lại có ����=����BCAB​=DCAD​ nên ����=����IAIH​=DCAD​. 

c) Ta có $△ABD\sim △HBI$ (g.g) 

suy ra ����=����⇒��.��=��.��HBAB​=BIBD​⇒AB.BI=BD.HB.

���^=���^BDA=BIH (hai góc tương ứng) 

mà ���^=���^BIH=AID (hai góc đối đỉnh)

suy ra ���^=���^BDA=AID 

do đó tam giác $AID$ cân tại $A$.

Cái này anh thấy có vẻ chưa đúng đề lắm em ạ

Vì 440 không chia hết cho 3 nên sao bằng được

`1/9(x-3)^2-1/25(x+5)^2=0`

`<=>(1/3x-1)^2-(1/5x+1)^2=0`

`<=>(1/3x-1-1/5x-1)(1/3x-1+1/5x+1)=0`

`<=>(2/15x-2). 8/15x=0`

`<=>2/15x-2=0` hoặc `8/15x=0`

`<=>x=15`         hoặc `x=0`

Vậy `S=`{`15;0`}