bạn hỏi thật hay hỏi đùa vậy 

 Bạn dụ dỗ cũng hấp dẫn đó nhưng không có số \(\overline{ab}\) nào thỏa mãn cả vì kể cả khi lấy trường hợp cho ra kết quả lớn nhất đối với số có 2 chữ số là \(99-10+99\) thì nó mới bằng \(188\). 

$96+79=95+80=175$

Cách giải: Ta thấy 79 cần 1 đơn vị nữa thì tròn 80, do đó ta thêm bớt như sau:

$96+79=96+(80-1)=(96-1)+80=95+80=175$

\(96+79=\left(96-1\right)+\left(79+1\right)=175\)

Tích của số chia và thương là: 10-3=7=7x1

=>Số chia là 7, thương là 1

Sửa đề : \(\dfrac{2025\times2024-1}{2023\times2025+2024}\)

\(=\)\(\dfrac{2025\times\left(2023+1\right)-1}{2023\times2025+2024}\)

\(=\dfrac{2025\times2023+2025-1}{2023\times2025+2024}\)

\(=\dfrac{2025\times2023+\left(2025-1\right)}{2023\times2025+2024}\)

\(=\dfrac{2025\times2023+2024}{2023\times2025+2024}\)

\(=1\)

@\(\text{格雷斯}\)

Bài 4:

a: \(\dfrac{9}{25}=\dfrac{18}{50}>\dfrac{17}{50}\)

=>Số học sinh đi xe buýt nhiều hơn đi xe đạp

b: Số học sinh đi bằng các phương tiện khác chiếm:

\(1-\dfrac{17}{50}-\dfrac{18}{50}=\dfrac{15}{50}\)

Vì \(\dfrac{15}{50}< \dfrac{17}{50}< \dfrac{18}{50}=\dfrac{9}{25}\)

nên số học sinh đi xe buýt là nhiều nhất

Bài 2:

a: \(\dfrac{5}{7}-\dfrac{3}{7}x=1\)

=>\(\dfrac{3}{7}x=\dfrac{5}{7}-1=-\dfrac{2}{7}\)

=>3x=-2

=>\(x=-\dfrac{2}{3}\)

b: \(x-\dfrac{-3}{4}=-\dfrac{14}{25}\)

=>\(x+\dfrac{3}{4}=-\dfrac{14}{25}\)

=>\(x=-\dfrac{14}{25}-\dfrac{3}{4}=\dfrac{-56}{100}-\dfrac{75}{100}=-\dfrac{131}{100}\)

c: \(\dfrac{5}{-20}-x=\dfrac{-7}{5}\)

=>\(x+\dfrac{1}{4}=\dfrac{7}{5}\)

=>\(x=\dfrac{7}{5}-\dfrac{1}{4}=\dfrac{28}{20}-\dfrac{5}{20}=\dfrac{23}{20}\)
d: \(x+\dfrac{3}{4}=\dfrac{36}{144}\cdot\dfrac{-12}{9}\)

=>\(x+\dfrac{3}{4}=\dfrac{1}{4}\cdot\dfrac{-4}{3}=-\dfrac{1}{3}\)

=>\(x=-\dfrac{1}{3}-\dfrac{3}{4}=\dfrac{-13}{12}\)

e: \(\dfrac{8}{23}\cdot\dfrac{46}{24}=\dfrac{1}{3}\cdot x\)

=>\(\dfrac{x}{3}=\dfrac{8}{24}\cdot\dfrac{46}{23}=\dfrac{2}{3}\)

=>x=2

f: \(\dfrac{1}{5}:x=\dfrac{1}{5}-\dfrac{1}{7}\)

=>\(\dfrac{1}{5}:x=\dfrac{2}{35}\)

=>\(x=\dfrac{1}{5}:\dfrac{2}{35}=\dfrac{1}{5}\cdot\dfrac{35}{2}=\dfrac{35}{10}=3,5\)

g: \(\dfrac{4}{9}-\left(x-\dfrac{1}{2}\right)^2=\dfrac{1}{3}\)

=>\(\left(x-\dfrac{1}{2}\right)^2=\dfrac{4}{9}-\dfrac{1}{3}=\dfrac{1}{9}\)

=>\(\left[{}\begin{matrix}x-\dfrac{1}{2}=\dfrac{1}{3}\\x-\dfrac{1}{2}=-\dfrac{1}{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{6}\\x=\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1}{6}\end{matrix}\right.\)

h: \(3,2x-\left(\dfrac{4}{5}+\dfrac{2}{3}\right):3\dfrac{2}{3}=\dfrac{7}{20}\)

=>\(3,2x-\dfrac{22}{15}:\dfrac{11}{3}=\dfrac{7}{20}\)

=>\(3,2x-\dfrac{22}{15}\cdot\dfrac{3}{11}=\dfrac{7}{20}\)

=>\(3,2x-\dfrac{2}{5}=\dfrac{7}{20}\)

=>\(3,2x=\dfrac{7}{20}+\dfrac{2}{5}=\dfrac{7}{20}+\dfrac{8}{20}=\dfrac{15}{20}=0,75\)

=>x=0,75:3,2=15/64

i: \(\left(4\dfrac{1}{2}-2x\right)\cdot1\dfrac{4}{61}=6\dfrac{1}{2}\)

=>\(\left(\dfrac{9}{2}-2x\right)\cdot\dfrac{65}{61}=\dfrac{13}{2}\)

=>\(\dfrac{9}{2}-2x=\dfrac{13}{2}:\dfrac{65}{61}=\dfrac{13}{2}\cdot\dfrac{61}{65}=\dfrac{61}{10}\)

=>2x=4,5-6,1=-1,6

=>x=-0,8

Lời giải:

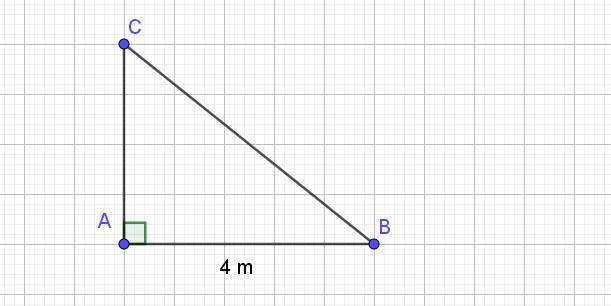
Ký hiệu gốc cây là $A$, ngọn cây bị gãy là $B$, điểm gãy là $C$. Ta có:

$AC+CB=8(1)$ (m)

$AB=4$ (m)

Áp dụng định lý Pitago:

$AC^2+AB^2=BC^2$

$\Rightarrow AC^2+4^2=BC^2$

$\Rightarrow BC^2-AC^2=16$

$\Rightarrow (BC-AC)(BC+AC)=16$

$\Rightarrow (BC-AC).8=16\Rightarrow BC-AC=2(2)$

Từ $(1); (2)\Rightarrow BC=(8+2):2=5; AC=(8-2):2=3$ (m)

Vậy độ dài từ điểm gãy tới gốc là $AC=3$ m

Hình vẽ:

`P=a^3+b^3+3ab`

`=(a+b)^3-3ab(a+b)+3ab`

`=1^3-3ab.1+3ab`

`=1`

Bài 3:

Tổng hai số lớn hơn số hạng thứ nhất 345 đơn vị nên số hạng thứ hai là 345.

Số hạng thứ nhất là:

\(345+77=422\)

Tổng hai số đó là:

\(422+345=767\)

Đáp số: 767

Bài 4:

Hiệu phép trừ đó là:

\(168+77=245\)

Số trừ là:

\(245-77=168\)

Số bị trừ trong phép trừ đó là:

\(245+168=413\)

Đáp số: 413

Bài 1:

Hiệu số gạo bác Tùng mua và số gạo bác Hai mua là:

\(19-4=15\left(kg\right)\)

Số gạo bác Tùng mua là:

\(345+15=360\left(kg\right)\)

Số gạo bác Hà mua là:

\(345-7=338\left(kg\right)\)

Đáp số: Bác Hai: 345 kg

            Bác Tùng: 360 kg

             Bác Hà: 338 kg

Bài 2:

Nếu ba ngày đều bán được 288 lít thì cửa hàng nhập về số lít bia là:

\(288\cdot3=864\left(l\right)\)

Cửa hàng nhập về số lít bia là:

\(864-29+\left(37-29\right)=843\left(l\right)\)

Đáp số: 843 l

\(\left(4x-5\right)\left(\dfrac{5}{4}x-2\right)=1\dfrac{1}{3}\)

=>\(5x^2-8x-\dfrac{25}{4}x+10-\dfrac{4}{3}=0\)

=>\(5x^2-\dfrac{57}{4}x+\dfrac{26}{3}=0\)

\(\Delta=\left(-\dfrac{57}{4}\right)^2-4\cdot5\cdot\dfrac{26}{3}=\dfrac{1427}{48}>0\)

=>Phương trình có hai nghiệm phân biệt là:

\(\left[{}\begin{matrix}x=\dfrac{\dfrac{57}{4}-\sqrt{\dfrac{1427}{48}}}{2\cdot5}=\dfrac{\dfrac{57}{4}-\dfrac{\sqrt{4281}}{12}}{10}=\dfrac{171-\sqrt{4281}}{120}\\x=\dfrac{171+\sqrt{4281}}{120}\end{matrix}\right.\)