ví dụ x=5 thì đâu có chia hết đâu, sai đề r b

 Biểu thức đại số biều thị quãng đường đi của ô tô là : 30.x

Biểu thức biểu thị quãng đường là : \(s=30t\left(km\right)\)

Sửa đề: Chiều rộng là x (m)

Do chiều dài gấp đôi chiều rộng nên chiều dài là 2x (m)

Diện tích hình chữ nhật là:

2x.x = 2x² (m²)

A B C H I E F

a/

Xét tg ABI và tg ACI có

AB=AC (cạnh bên tg cân)

\(\widehat{BAH}=\widehat{CAH}\) (trong tg cân đường cao hạ từ đỉnh tg cân đồng thời là đường phân giác của góc ở đỉnh)

AI chung

=> tg ABI = tg ACI (c.g.c) => IB=IC => tg IBC cân

b/

tg ABI = tg ACI (cmt) \(\Rightarrow\widehat{AIB}=\widehat{AIC}\)

c/ Xét tg IBF và tg ICE có

\(\widehat{BIF}=\widehat{CIE}\) (góc đối đỉnh)

IB=IC (cmt)

tg ABI = tg ACI (cmt) \(\Rightarrow\widehat{ABI}=\widehat{ACI}\)

=> tg IBF = tg ICE => IE=IF

d/

Ta có

IE=IF (cmt) => tg IEF cân tại I

\(\Rightarrow\widehat{IEF}=\widehat{IFE}=\dfrac{180^o-\widehat{FIE}}{2}\) (1)

Xét tg cân IBC có

\(\widehat{IBC}=\widehat{ICB}=\dfrac{180^o-\widehat{BIC}}{2}\) (2)

Mà \(\widehat{FIE}=\widehat{BIC}\) (góc đối đỉnh) (3)

Từ (1) (2) (3) \(\Rightarrow\widehat{IFE}=\widehat{ICB}\) Hai góc này nằm ở vị trí so le trong

=> EF//BC

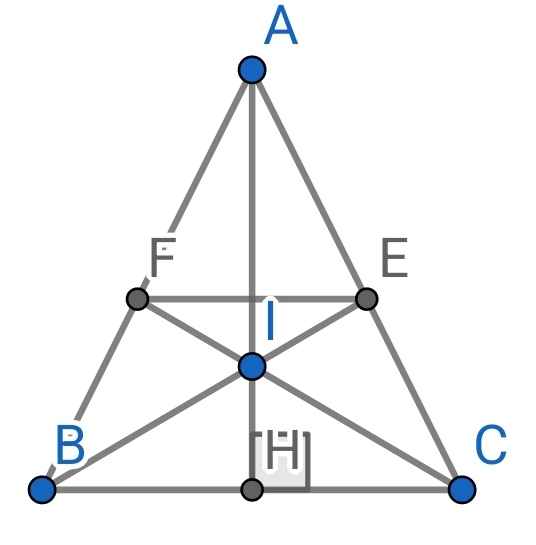 a) ∆ABC cân tại A (gt)

AH là đường cao (gt)

⇒ AH cũng là đường trung trực của ∆ABC

⇒ AH là đường trung trực của BC

I ∈ AH (gt)

⇒ IB = IC

⇒ ∆IBC cân tại I

b) Xét ∆AIB và ∆AIC có:

AI là cạnh chung

AB = AC (do ∆ABC cân tại A)

IB = IC (cmt)

⇒ ∆AIB = ∆AIC (c-c-c)

⇒ ∠AIB = ∠AIC (hai góc tương ứng)

c) Do ∆AIB = ∆AIC (cmt)

⇒ ∠ABI = ∠ACI (hai góc tương ứng)

⇒ ∠FBI = ∠ECI

Xét ∆BIF và ∆CIE có:

∠FBI = ∠ECI (cmt)

IB = IC (cmt)

∠FIB = ∠EIC (đối đỉnh)

⇒ ∆BIF = ∆CIE (g-c-g)

⇒ IF = IE (hai cạnh tương ứng)

Hay IE = IF

d) ∆IBC cân tại I (cmt)

IH là đường trung trực của BC (cmt)

⇒ IH cũng là đường phân giác của ∆IBC

⇒ ∠BIH = ∠CIH

Ta có:

∠AIE = ∠BIH (đối đỉnh)

∠AIF = ∠CIH (đối đỉnh)

Mà ∠BIH = ∠CIH (cmt)

⇒ ∠AIE = ∠AIF

Xét ∆AIE và ∆AIF có:

IE = IF (cmt)

∠AIE = ∠AIF (cmt)

AI là cạnh chung

⇒ ∆AIE = ∆AIF (c-g-c)

⇒ AE = AF (hai cạnh tương ứng)

⇒ A nằm trên đường trung trực của EF (1)

Do IE = IF (cmt)

⇒ I nằm trên đường trung trực của EF (2)

Từ (1) và (2) ⇒ AI là đường trung trực của EF

⇒ AI ⊥ EF

⇒ AH ⊥ EF

Mà AH ⊥ BC (gt)

⇒ EF // BC

Ta có: 

\(\widehat{xOt}=\widehat{zOy}\)

Mà: 

\(\widehat{xOt},\widehat{zOy}\) có chung \(\widehat{zOt}\)

`=>` \(\widehat{xOz}=\widehat{tOy}\) `(đpcm)`

Ta có \(\left(x-y\right)^2\ge0;\left(y-z\right)^2\ge0;\left(z-1\right)^2\ge0\)

Để bth bằng 0 

=> \(\left\{{}\begin{matrix}\left(x-y\right)^2=0\\\left(y-z\right)^2=0\\\left(z-1\right)^2=0\end{matrix}\right.\Rightarrow x=y=z=1\)

\(\left(7x+2\right)^{-1}=3^{-2}\)

=>\(\dfrac{1}{7x+2}=\dfrac{1}{3^2}=\dfrac{1}{9}\)

=>7x+2=9

=>7x=7

=>x=1

1: (2x-1)*x>0

TH1: \(\left\{{}\begin{matrix}2x-1>0\\x>0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>\dfrac{1}{2}\\x>0\end{matrix}\right.\Leftrightarrow x>\dfrac{1}{2}\)

TH2: \(\left\{{}\begin{matrix}2x-1< 0\\x< 0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< \dfrac{1}{2}\\x< 0\end{matrix}\right.\)

=>x<0

2: 
ĐKXĐ: x<>1

\(\dfrac{x+3}{x-1}< 0\)

TH1: \(\left\{{}\begin{matrix}x+3>0\\x-1< 0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>-3\\x< 1\end{matrix}\right.\)

=>-3<x<1

TH2: \(\left\{{}\begin{matrix}x+3< 0\\x-1>0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x< -3\\x>1\end{matrix}\right.\)

=>Loại

c: 

ĐKXĐ: x<>0

\(\dfrac{x^2-2}{5x}< 0\)

TH1: \(\left\{{}\begin{matrix}x^2-2< 0\\5x>0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x^2< 2\\x>0\end{matrix}\right.\Leftrightarrow0< x< \sqrt{2}\)

TH2: \(\left\{{}\begin{matrix}x^2-2>0\\5x< 0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x^2>2\\x< 0\end{matrix}\right.\Leftrightarrow-\sqrt{2}< x< 0\)

d: (x-3)(x+7)>0

TH1: \(\left\{{}\begin{matrix}x-3>0\\x+7>0\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}x>3\\x>-7\end{matrix}\right.\Leftrightarrow x>3\)

TH2: \(\left\{{}\begin{matrix}x-3< 0\\x+7< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< 3\\x< -7\end{matrix}\right.\)

=>x<-7

Sửa đề:

 \(3^{2n+3}-3^{2n+2}=2\cdot3^{10}\\ \Rightarrow3^{2n+2}\cdot3-3^{2n+2}=2\cdot3^{10}\\ \Rightarrow3^{2n+2}\cdot\left(3-1\right)=2\cdot3^{10}\\ \Rightarrow2\cdot3^{2n+2}=2\cdot3^{10}\\ \Rightarrow3^{2n+2}=3^{10}\\ \Rightarrow2n+2=10\\ \Rightarrow2n=8\\ \Rightarrow n=4\)

Vậy...
 

\(5^{n+3}-5^{n+1}=5^{12}.120\)

\(\Leftrightarrow5^n.5^3-5^n.5=5^{12}.120\Leftrightarrow5^n\left(5^3-5\right)=5^{12}.120\Leftrightarrow5^n.120=5^{12}.120\Leftrightarrow5^n=5^{12}\Rightarrow n=12\)