 Mình cảm ơn!! Cần giải gấp
Mình cảm ơn!! Cần giải gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Khối lượng hạt cà phê khô thu được là:
420:(20:5)=420:4=105(kg)

Bài 22:
a: Diện tích 1 ô trồng hoa là \(a^2\left(m^2\right)\)
Diện tích trồng hoa là \(4\cdot a^2\left(m^2\right)\)
Diện tích đất trồng rau là: \(20^2-4a^2=400-4a^2\left(m^2\right)\)
b: Diện tích đất trồng hoa bằng diện tích đất trồng rau
=>\(4a^2=400-4a^2\)
=>\(8a^2=400\)
=>\(a^2=50\)
=>\(a=5\sqrt{2}\)
c:
Số tiền lãi khi trồng hoa là: \(20000\cdot4a^2=80000a^2\left(đồng\right)=80a^2\left(nghìnđồng\right)\)
Số tiền lãi khi trồng rau là: \(15\cdot\left(400-4a^2\right)=6000-60a^2\)(nghìn đồng)
Số tiền lãi trồng hoa bằng 3/4 số tiền lãi trồng rau nên ta có:
\(80a^2=\dfrac{3}{4}\left(6000-60a^2\right)\)
=>\(80a^2=4500-45a^2\)
=>\(125a^2=4500\)
=>\(a^2=36\)
=>Diện tích đất trồng hoa là \(4a^2=144\left(m^2\right)\)

Trong 1 giờ, vòi 1 chảy được: \(\dfrac{1}{3}\left(bể\right)\)
Trong 1 giờ, vòi 2 chảy được: \(\dfrac{1}{2}\left(bể\right)\)
Vì \(\dfrac{1}{2}>\dfrac{1}{3}\) nên trong 1 giờ, vòi 2 chảy được nhiều hơn vòi 1 là \(\dfrac{1}{2}-\dfrac{1}{3}=\dfrac{1}{6}\left(bể\right)\)

a: \(A=2n^2+n-3\)
\(=2n^2+3n-2n-3\)
\(=n\left(2n+3\right)-\left(2n+3\right)=\left(2n+3\right)\left(n-1\right)\)
Nếu n=0 thì \(A=\left(2\cdot0+3\right)\left(0-1\right)=-3< 0\)
=>Loại
Nếu n=1 thì \(A=\left(2\cdot1+3\right)\left(1-1\right)=0\)
=>Loại
Nếu n=2 thì \(A=\left(2\cdot2+3\right)\left(2-1\right)=7\) là số nguyên tố
=>Nhận
Khi n>2 thì \(A=\left(2n+3\right)\left(n-1\right)\) là tích của 2 số tự nhiên lớn hơn 1
=>A không phải là số nguyên tố
=>Loại
b: \(B=n^4+n^2+1=n^4+2n^2+1-n^2\)
\(=\left(n^2+1\right)^2-n^2=\left(n^2-n+1\right)\left(n^2+n+1\right)\)
Khi n=0 thì \(B=\left(0^2-0+1\right)\left(0^2+0+1\right)=1\)
=>Loại
Khi n=1 thì \(B=\left(1^2-1+1\right)\left(1^2+1+1\right)=3\) là số nguyên tố
=>Nhận
Khi n>1 thì \(B=\left(n^2-n+1\right)\left(n^2+n+1\right)\) là tích của hai số tự nhiên lớn hơn 1
=>Loại

Gọi số nhãn vở của Chi là x(nhãn)
(Điều kiện: \(x\in Z^+\))
Trung bình cộng số nhãn vở của 3 bạn là \(\dfrac{x+20+20}{3}=\dfrac{x+40}{3}\)
Chi có số nhãn vở ít hơn trung bình cộng của 3 bạn là 6 cái nên ta có:
\(\dfrac{x+40}{3}-x=6\)
=>\(\dfrac{x+40-3x}{3}=6\)
=>-2x+40=18
=>-2x=-22
=>x=11(nhận)
Vậy: Chi có 11 nhãn vở
Gọi số nhãn vở của Chi là \(x\) (nhãn) (\(x\inℕ^∗\))
Ta có: Trung bình cộng số nhãn vở của 3 bạn là:
\(\dfrac{x+20+20}{3}=\dfrac{x+40}{3}\)
Vì Chi có số nhãn vở ít hơn trung bình cộng của ba bạn 6 cái nên:
\(x-\dfrac{x+40}{3}=6\)
\(3x-\left(x+40\right)=18\)
\(2x-40=18\)
\(2x=58\)
\(x=29\) (nhãn) (thỏa mãn điều kiện)
Vậy Chi có \(29\) nhãn vở.

`#3107.101107`
`(a + b + c)^2 = a^2 + b^2 + c^2`
`\Rightarrow (a + b + c)^2 - (a^2 + b^2 + c^2) = 0`
`\Rightarrow a^2 + b^2 + c^2 + 2ab + 2bc + 2ca - a^2 - b^2 - c^2 = 0`
`\Rightarrow 2ab + 2bc + 2ca = 0`
`\Rightarrow 2(ab + bc + ca) = 0`
`\Rightarrow ab + bc + ca = 0`
\(\Rightarrow\dfrac{ab+bc+ca}{abc}=0\\ \Rightarrow\dfrac{ab}{abc}+\dfrac{bc}{abc}+\dfrac{ca}{abc}=0\\ \Rightarrow\dfrac{1}{c}+\dfrac{1}{a}+\dfrac{1}{b}=0\)
Đặt \(x=\dfrac{1}{a};y=\dfrac{1}{b};z=\dfrac{1}{c}\)
`=> x + y + z = 0`
`=> x + y = -z` (*)
`=> (x + y)^3 = -(z)^3`
`=> x^3 + y^3 + 3xy(x + y) = -z^3`
Thay (*) vào bt
`=> x^3 + y^3 + z^3 + 3xy(-z) = 0`
`=> x^3 + y^3 + z^3 - 3xyz = 0`
`=> x^3 + y^3 + z^3 = 3xyz`
`=>`\(\dfrac{1}{a^3}+\dfrac{1}{b^3}+\dfrac{1}{c^3}=\dfrac{3}{abc}\left(\text{đpcm}\right).\)

$53\times x-34=135: 1\frac78$
$53\times x-34=135:\frac{15}{8}$
$53\times x-34=72$
$53\times x=72+34$
$53\times x=106$
$x=106:53$
$x=2$

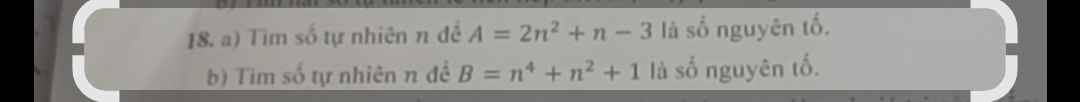
a/
$A=x^2-4x+10=(x^2-4x+4)+6=(x-2)^2+6$
Ta thấy:
$(x-2)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A=(x-2)^2+6\geq 6>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow A$ luôn có giá trị dương với mọi giá trị $x$.
a/
$B=2x^2-2x+3=x^2+(x^2-2x+1)+2=x^2+(x-1)^2+2$
Ta thấy:
$x^2\geq 0; (x-1)^2\geq 0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B=x^2+(x-1)^2+2\geq 2>0$ với mọi $x\in\mathbb{R}$
$\Rightarrow B$ luôn có giá trị dương với mọi giá trị $x$.