Kéo dài CD, BE sao cho chúng cắt đường thẳng song song với BC đi qua A  lần lượt tại K, G.

Xét \(\Delta NMC\) có: \(AK//MC\text{ (}AK//BC;M\in BC)\)

\(\Rightarrow\dfrac{AN}{NM}=\dfrac{AK}{MC}\) (hệ quả đli Talet) (1)

Xét \(\Delta NMB\) có: \(AG//MB\text{ (}AG//BC;M\in BC)\)

\(\Rightarrow\dfrac{AN}{NM}=\dfrac{AG}{MB}\) (hệ quả đli Talet) (2)

Từ (1) và (2) \(\Rightarrow\dfrac{AK}{MC}=\dfrac{AG}{MB}\)

Mà \(MB=MC\) (vì M là trung điểm BC) nên \(AK=AG\) (3)

Xét \(\Delta BDC\) có: \(AK//BC\Rightarrow \dfrac{AD}{BD}=\dfrac{AK}{BC}\) (hệ quả đli Talet) (4)

Xét \(\Delta CEB\) có: \(AG//BC\Rightarrow \dfrac{AE}{EC}=\dfrac{AG}{BC}\) (hệ quả đli Talet) (5)

Từ (3), (4) và (5) \(\Rightarrow\dfrac{AD}{BD}=\dfrac{AE}{EC}\Rightarrow\dfrac{AD}{AD+BD}=\dfrac{AE}{AE+EC}\)

\(\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)

Xét \(\Delta ABC\) có: \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) (cmt) \(\Rightarrow DE//BC\) (đli Talet đảo)

\(\rightarrow\) Chọn C. Cả A và B đều đúng

$Toru$

Theo đề bài, ta có \(\overline{qr}+2\overline{ppp}=2022\) 

\(\Leftrightarrow\overline{ppp}=\dfrac{2022-\overline{qr}}{2}\) \(\ge\dfrac{2022-99}{2}=961,5\) hay \(\overline{ppp}\ge962\)

Do đó \(\overline{ppp}=999\)

Khi đó \(\overline{qr}=2022-2\overline{ppp}=2022-2.999=24\)

Vậy \(p=9,q=2,r=4\)

Mình nghĩ là bằng nhau.

`060° = 60°`nhé

\(x+\sqrt{x+2}=0\left(ĐK:x\ge-2\right)\)

\(\Leftrightarrow x+1+\left(\sqrt{x+2}-1\right)=0\\ \Leftrightarrow x+1+\dfrac{x+2-1}{\sqrt{x+2}+1}=0\\ \Leftrightarrow x+1+\dfrac{x+1}{\sqrt{x+2}+1}=0\\ \Leftrightarrow\left(x+1\right)\left(1+\dfrac{1}{\sqrt{x+2}+1}\right)=0\\ \Rightarrow\left[{}\begin{matrix}x+1=0\\1+\dfrac{1}{\sqrt{x+2}+1}=0\left(PTVN\right)\end{matrix}\right.\Leftrightarrow x=-1\left(TMDK\right)\)

Vậy pt có nghiệm duy nhất: x=-1

Mình giải thích thêm phần này nhé:

\(1+\dfrac{1}{\sqrt{x+2}+1}=0\left(PTVN\right)\)

Vì với mọi x thuộc ĐK:

\(\sqrt{x+2}\ge0\Rightarrow\sqrt{x+2}+1>0\\ \Rightarrow\dfrac{1}{\sqrt{x+2}+1}>0\\ \Rightarrow VT=1+\dfrac{1}{\sqrt{x+2}+1}>0=VP\)

Do VT > VP nên không thể xảy ra dấu = 

Dẫn đến ptvn bạn nhé

Tổng của 704 và 516 là:

  704 + 516 = 1220

Số Linh nghĩ là:

  1220 : 4 = 305

    Đáp số: 305

Tổng 2 số 704 và 516 là:

\(704+516=1220\)

Số Linh nghĩ ra là:

\(1220:4=305\)

Đáp số: 305

Bài toán được mô tả như hình sau:

Sửa đề: chuyển cm thành m

Độ dài đáy bé được mở rộng thêm là:

\(600:\dfrac{1}{2}:30=40\left(m\right)\)

Độ dài đáy bé của thửa ruộng là:

\(160-40=120\left(m\right)\)

Diện tích thửa ruộng là:

\(\dfrac{\left(160+120\right)\times30}{2}=4200\left(m^2\right)=0,42\left(ha\right)\)

Năm 2023 số tiền hoa anh Nam thu được trên thửa ruộng đó là:

\(0,42\times650000000=273000000\) (đồng)

Số Lan dùng để nhân với 9 là:

   \(1242:6=207\)

Tích đúng là:

   \(207\times9=1863\)

Ta có: \(22\equiv1\left(\text{mod }3\right)\Rightarrow22^{22}\equiv1^{22}\equiv1\left(\text{mod }3\right)\)

\(\Rightarrow22^{22}-1\equiv0\left(\text{mod }3\right)\)

hay \(22^{22}-\text{1 } \vdots \text{ 3}\)

Dòng chữ TOQUOCVIETNAM có 13 chữ cái và lặp đi lặp lại

Do 2018 : 13 = 155 (dư 3) nên chữ cái thứ 2018 là chữ cái thứ 3 trong dãy TOQUOCVIETNAM nên là chữ Q

Chọn C

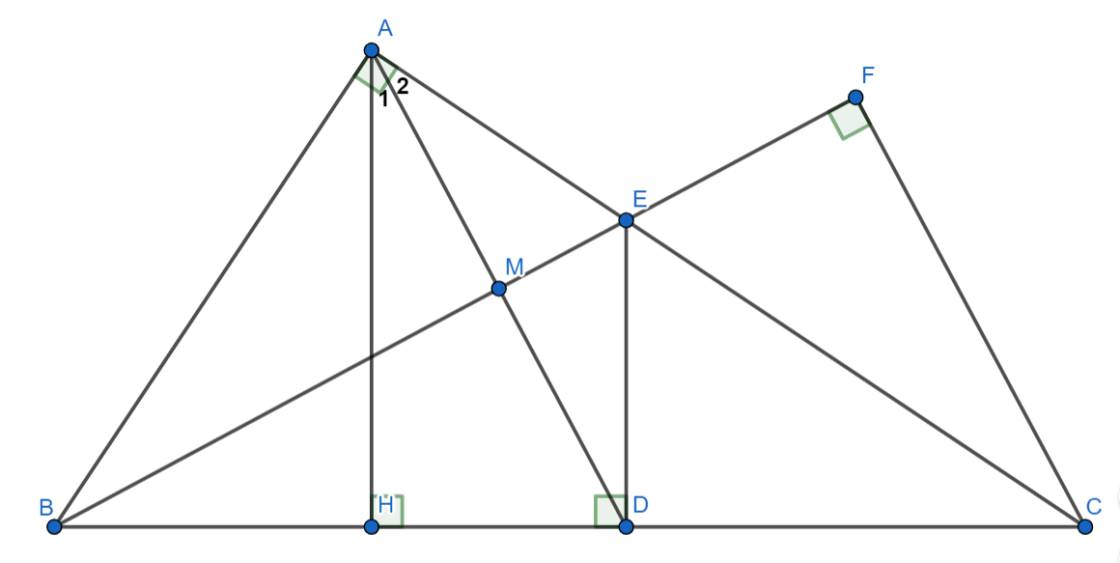
a) Xét \(\Delta BAE\) và \(\Delta BDE\) có:  

\(\left\{{}\begin{matrix}\widehat{BAE}=\widehat{BDE}=90^{\circ}\left(\Delta ABC\text{ vuông tại }A;DE\perp BC\right)\\BE\text{ chung}\\BA=BD\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow\Delta BAE=\Delta BDE\left(ch-cgv\right)\) (đpcm)

b) Ta có: \(BD=BA\Rightarrow B\) là điểm nằm trên đường trung trực của AD (1)

Vì \(\Delta BAE=\Delta BDE\left(cmt\right)\Rightarrow AE=DE\) (2 cạnh tương ứng)

\(\Rightarrow E\) là điểm nằm trên đường trung trực của AD (2)

Từ (1) và (2) \(\Rightarrow BE\) là đường trung trực của AD

Mà: \(BE\cap AD=\left\{M\right\}\) nên \(BM\perp AD\)

hay \(BM\) là đường cao của \(\Delta ABD\) (đpcm)

c) Vì \(AE=DE\Rightarrow\Delta ADE\) cân tại E (t/c)

\(\Rightarrow\widehat{A_2}=\widehat{EDA}\) (t/c) (3)

Lại có: \(\begin{cases} AH\perp CD\\ DE\perp CD \end{cases} \Rightarrow AH//DE\)

\(\Rightarrow\widehat{A_1}=\widehat{EDA}\) (2 góc so le trong) (4)

Từ (3) và (4) \(\Rightarrow\widehat{A_1}=\widehat{A_2}\)

Mà tia AD nằm trong \(\widehat{HAC}\)

nên tia AD là tia phân giác của \(\widehat{HAC}\) (đpcm)

d) Xét \(\Delta EBC\) có: \(\left\{{}\begin{matrix}AB\perp EC\left(\Delta ABC\text{ vuông tại }A;E\in AC\right)\\DE\perp BC\left(gt\right)\\CF\perp BE\left(gt\right)\end{matrix}\right.\)

\(\Rightarrow AB,DE,CF\) đồng quy (t/c) (đpcm)

$\text{#}Toru$

$Toru$